Question

What are forced vibrations and resonance? Show that only odd harmonics are present in an air column vibrating in a pipe closed at one end. A stretched wire emits a fundamental note of frequency $256Hz$. Keeping the stretching force constant and reducing the length of wire by $10cm$, the frequency becomes $320Hz$. Calculate the original length of wire.

Answer 1

To solve this question, we need to use the relation between the frequency and the length of a stretched string from $f = \dfrac{v}{\lambda }$. Then on putting the given values provided in the question, we will get the final answer.

Formula used: The formulae used to solve this question are given by
\Rightarrow A = \dfrac{F}{{{{\left\\{ {{m^2}{{\left( {{\omega ^2} - \omega _d^2} \right)}^2} + \omega _d^2{b^2}} \right\\}}^{1/2}}}} , here $A$ is the amplitude, $F$ is the amplitude of the external driving force, $\omega$ is the natural frequency, and ${\omega _d}$ is the driving frequency.
$\Rightarrow f = \dfrac{v}{\lambda }$, here $f$ is the frequency, $v$ is the velocity, and $\lambda$ is the wavelength of a wave.
$\Rightarrow v = \sqrt {\dfrac{T}{\mu }}$, here $v$ is the velocity of the wave in a string which has a mass per unit length of $\mu$, and is stretched by a force of $T$.

Complete step by step answer
When a system oscillates in a medium, there is some amount of damping present in the system, which eventually finishes out the oscillation. This damping is due to the viscous force of water, drag force of air etc. which always acts opposite to the relative motion of the system. So, to maintain the oscillations, we apply external periodic force. Then the system oscillates with the frequency equal to the frequency of the force, as the natural oscillations die out due to damping. These oscillations or vibrations are known as forced vibrations.
The amplitude in the forced vibrations is given by
\Rightarrow A = \dfrac{F}{{{{\left\\{ {{m^2}{{\left( {{\omega ^2} - \omega _d^2} \right)}^2} + \omega _d^2{b^2}} \right\\}}^{1/2}}}}
We can clearly observe that when the driving frequency is very much close to the natural frequency, then amplitude becomes maximum, which is given by
$\Rightarrow A = \dfrac{F}{{{\omega _d}b}}$
This phenomenon of maximising the amplitude, by setting the driving frequency close to the natural frequency is termed as resonance.
Let us consider an air column of length $L$ which is closed at one end. We know that there is node formation at the closed end and an antinode at the open end. So for the fundamental harmonic, we consider the below diagram.

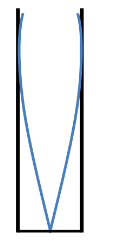
We know that the distance between a node and an antinode is equal to $\dfrac{\lambda }{2}$. So we have
$\Rightarrow \dfrac{\lambda }{2} = L$
$\Rightarrow \lambda = 2L$ ……………………….(1)
We know that the frequency is given by
$\Rightarrow f = \dfrac{v}{\lambda }$
So from (1) the fundamental frequency is
$\Rightarrow {f_0} = \dfrac{v}{{2L}}$ ……………………….(2)
Now, let us consider the air column for the first overtone.

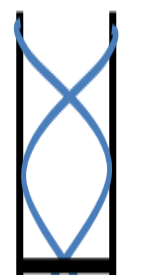
For this case, we have
$\Rightarrow L = \dfrac{{3\lambda }}{2}$
$\Rightarrow \lambda = \dfrac{{2L}}{3}$
So the first overtone frequency becomes
$\Rightarrow {f_1} = \dfrac{{3v}}{{2L}}$
From (2)
$\Rightarrow {f_1} = 3{f_0}$
Similarly, for the ${n^{th}}$ overtone, the frequency is given by
$\Rightarrow {f_n} = \left( {2n + 1} \right){f_0}$
So we see from the above expression that the overtone frequencies are the odd multiples of the fundamental frequency. So, only odd harmonics are present in an air column vibrating in a pipe closed at one end.
We know that the velocity of wave in a stretched string is given by
$\Rightarrow v = \sqrt {\dfrac{T}{\mu }}$
The fundamental frequency of the wave in a stretched string is given by
$\Rightarrow f = \dfrac{1}{{2L}}\sqrt {\dfrac{T}{\mu }}$
According to the question, the frequency is given as $256Hz$. So we have
$\Rightarrow 256 = \dfrac{1}{{2L}}\sqrt {\dfrac{T}{\mu }}$ ……………………….(3)
Now, when the length is reduced by $10cm$, the frequency becomes $320Hz$. So we have
$\Rightarrow 320 = \dfrac{1}{{2\left( {L - 10} \right)}}\sqrt {\dfrac{T}{\mu }}$ ……………………….(4)
Dividing (4) by (3) we get
$\Rightarrow \dfrac{{320}}{{256}} = \dfrac{{\dfrac{1}{{2\left( {L - 10} \right)}}\sqrt {\dfrac{T}{\mu }} }}{{\dfrac{1}{{2L}}\sqrt {\dfrac{T}{\mu }} }}$
$\Rightarrow \dfrac{5}{4} = \dfrac{L}{{\left( {L - 10} \right)}}$
On solving the above equation, we get the original length of the wire as
$\Rightarrow L = 50cm$

Hence, the original length of the wire is equal to $50cm$.

Note
There will be no change in the velocity of the wave in the stretched wire given in the question. The tension is already given to be constant. And the mass per unit length will also not change, as it is the property of material of the wire.