Solveeit Logo
Login

Question

Question: What are conservative forces?...

What are conservative forces?

Explanation

Solution

Hint Conservative force has a property that work done in moving a particle between two points is independent of the path taken.

Complete step-by-step solution :The work done by such forces
Does not depend upon path.
Depends only and only initial and final position.
For example:- If A and B are the two points and a conservative force acts on point A and B. Then we assume the three ways to go at point B . 1,2 and 3 are the three ways.

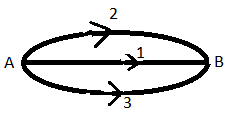
If the force is conservative, then work done by this force by first path, by second path and third path are equal.
Let W1{{W}_{1}} be the work done along path 1, W2{{W}_{2}} be the work done along path 2 and W3{{W}_{3}} be the work done along path 3
Then,
W1=W2=W3{{W}_{1}}={{W}_{2}}={{W}_{3}}
Examples of conservative forces are gravitational force , spring force, and electrostatic force.
First we talk about gravitational force, let us assume (m)\left( m \right) .Which is placed on an inclined plane.
For path 1:-
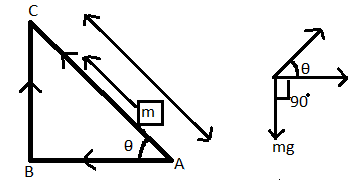
Angle between force (mg)\left( mg \right) and displacement (l)\left( l \right) is(90∘+θ)\left({{90}^{\circ }}+\theta \right)

Than W1=FScos⁡ϕ W1=mgl(cos⁡(90∘+θ))  \begin{aligned} & {{W}_{1}}=FS\cos \phi \\\ & {{W}_{1}}=mgl\left( \cos \left( {{90}^{\circ }}+\theta \right) \right) \\\ & \\\ \end{aligned} [cos⁡(90∘+θ)=−sin⁡θ]\left[ \cos \left( {{90}^{\circ }}+\theta \right)=-\sin \theta \right]
W1=−mglsin⁡θ{{W}_{1}}=-mgl\sin \theta …………………..(i)
For path 2
First we go from point A to point B and then from point B to point C.
W=WAB+WBCW={{W}_{AB}}+{{W}_{BC}}
When we go from A to B then the angle between force and displacement is 90∘{{90}^{\circ }} (cos⁡90∘=0)\left( \cos {{90}^{\circ }}=0 \right) .
Than WAB=FScos⁡90∘ WAB=0 \begin{aligned} & {{W}_{AB}}=FS\cos {{90}^{\circ }} \\\ & {{W}_{AB}}=0 \\\ \end{aligned}
When we go from point B to C then the angle between force and displacement is 180∘{{180}^{{}^\circ }}.
WBC=−mglsin⁡θ{{W}_{BC}}=-mgl\sin \theta
W2=WAB+WBC{{W}_{2}}={{W}_{AB}}+{{W}_{BC}}
W2=−mglsin⁡θ{{W}_{2}}=-mgl\sin \theta ……………….. (ii)
W1=W2{{W}_{1}}={{W}_{2}}
So the work done in the first path is equal to work done in the second path. So it is independent of path.

Note:
Students think that whose path has long distance then work done is maximum for that path, but for conservative force work done does not depend on path distance.