Question
Question: What are conjugate foci? Deduce the following expression between the focal length \(f\), of a spheri...
What are conjugate foci? Deduce the following expression between the focal length f, of a spherical mirror, distance of the object u and image v
f1=u1+v1.
Solution
Hint: Conjugate foci are points such that if we keep an object at one point, we get the rays focused on the other point and vice-versa. The mirror formula is derived by considering similar triangles in the ray diagram.
Complete step-by-step solution -
We know that light rays from a point A on the principal axis, after refraction from the lens, focus at another single point B on the axis.
Also, if we interchange these points and keep the source at B, the rays would focus at A. All such pairs of interchangeable points that are related as Source and image are called conjugate foci.
It is called foci because light from one such point focuses on the other.
Let us imagine a mirror, as shown in figure, which forms a real image of a source. Let us call the distance of the object from the pole u and that of image from the pole v. Also, let the focal length of the mirror be given as f.
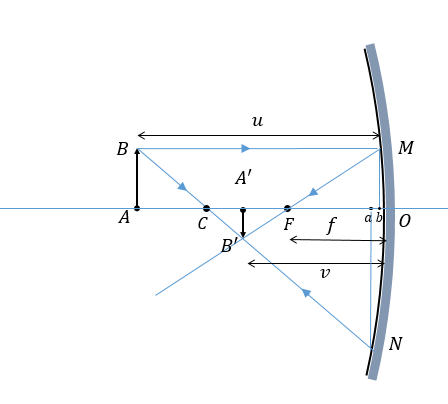
Let's draw two perpendiculars - from points M and N. Let these lines meet the principal axis at a and b respectively. For thin mirrors, a and b would be very close to each other and also close to the pole O So we can approximate a and b to O
To find the relation between v and u, let us consider the triangles ΔABC and ΔA′B′C
we see that
∠ACB=∠A′CB′ since they are vertically opposite.
∠ABC=∠A′B′C=90o
So we can say that ΔABC and ΔA′B′Care similar by AA criterion.
Now, since the corresponding parts of two similar triangles have the same ratio:
A′B′AB=A′CAC (1)
Now let us consider triangles ΔMOF and ΔA′B′F
we see that
∠MFO=∠A′FB′ since they are vertically opposite.
∠MOF=∠A′B′F=90o
So we can say that ΔMOF and ΔA′B′Fare similar by AA criterion.
Now, since the corresponding parts of two similar triangles have the same ratio:
A′B′MO=A′FOF
But OM and AB are equal. So we can say that:
A′B′AB=A′FOF (2)
Let us compare (1) and (2)
A′CAC=A′FOF
Now we can substitute the values of AC , A′C. , OF and A′F from figure.
AC=OA−OC=u−R
A′C=OC−OA′=R−v
A′F=OA′−OF=v−f
OF=f
but we should apply sign conventions while measuring distances. All distances measured to the left are negative.
So,
AC=−(u−R)
A′C=−(R−v)
A′F=−(v−f)
OF=−f
So we can substitute these values into equation (3) to get:
−(R−v)−(u−R)=−(v−f)−f
(v−f)(u−R)=f(R−v)
uv−vR−fu+fR=fR−fv
Since R=2f, uv−2vf−fu=−fv
uv−fu=fv
We can divide this equation by uvf to get :f1−v1=u1
Thus, f1=u1+v1
Note: There are infinitely many conjugate foci for mirrors and lenses. The centre of curvature of a mirror is a special point for which the image and object positions coincide. Also note that the same derivation can also be done for convex mirrors. proper sign conventions have to be used for u, v and f.
