Question

What Are Barkhausen Conditions For Oscillation?

Answer 1

An oscillator is a circuit, it produces a repeated, alternating waveform without any input. Oscillators work on the principle of positive feedback. A small fraction of the output of the amplifier is fed back to the input. so that the output generates continuously even though the input was removed. We are going to discuss the Barkhausen conditions for oscillation.

Complete answer:
For oscillator, the voltage gain of an amplifier is given by,
${V_f} = \dfrac{A}{{1 - \beta .A}}$
Where,${V_f}$ - voltage gain with feedback
A-voltage gain without feedback
$\beta .A$-loop gain

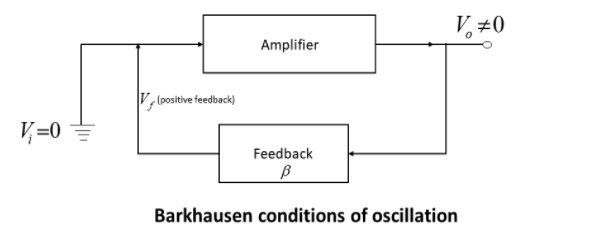
The firstBarkhausen condition is that the overall loop gain should be unity
$\beta .A = 1$
By applying the above condition in the voltage gain of an amplifier,
${V_f} = \dfrac{A}{{1 - 1}}$
${V_f} = \dfrac{A}{0}$
${V_f} = \infty$
We know that the voltage gain of the amplifier is
${V_f} = \dfrac{{{V_o}}}{{{V_i}}}$
Where ${V_o}$- output voltage
${V_i}$- input voltage
If the voltage gain of the amplifier with feedback is infinity,
$\dfrac{{{V_o}}}{{{V_i}}} = \infty$
${V_i} = 0$, the input voltage becomes zero.
Therefore, $\beta .A = 1$ it is the condition to sustained oscillations
The second condition of Barkhausen conditions is that the total phase shift around loop gain should be ${0^ \circ }$ or ${360^ \circ }$
It is attained by positive feedback to the amplifier. The part of the output signal is fed back to the input signal which should be the same in phase with an input signal.
The two Barkhausen conditions of oscillation are (i) the overall loop gain should be unity and (ii) the total phase shift around loop gain should be ${0^ \circ }$ or ${360^ \circ }$

Note: From these conditions, the oscillator will produce sustained oscillations and will generate a sinusoidal signal. The Barkhausen condition is used in electronic circuits to find whether the circuit will oscillate or not. The feedback signal and the input signal are in phase for producing oscillations by giving positive feedback to the amplifier. If $\beta .A > 1$, the input voltage becomes positive and the amplitude of the oscillation will be increased.