Question

What are (a) the x-component and (b) y-component of a vector $\vec a$ in the xy plane if is direction is ${250^ \circ }$ counterclockwise from the positive direction of the x-axis and its magnitude is given as $7.3{\text{ m ?}}$

Answer 1

The magnitude of vector $\vec a$ is given. We have to find its x and y components. For any vector the x component of a vector is basically the product of the magnitude of the vector and the cosine of the angle which it makes with the positive direction of the x-axis. The direction of angle here is counter clockwise which means anti-clockwise.

Complete step by step answer:
Since we know that the x component of a vector is the product of the magnitude of the vector and the cosine of the angle which it makes with the positive direction of the x-axis.

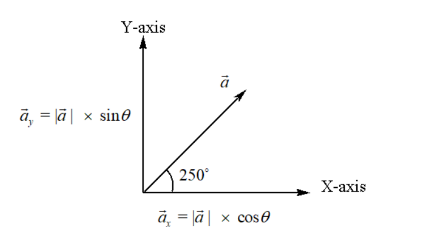
(a) Let us assume ${\vec a_x}$ represents the x component of vector $\vec a$ then it can be represented as,
${\vec a_x}{\text{ = |}}\vec a|{\text{ }} \times {\text{ cos}}\theta$
Where, ${\text{|}}\vec a|$ represents the magnitude of the vector $\vec a$ and $\theta$ is the angle between the vector and positive x axis.

According to question, ${\text{|}}\vec a|{\text{ = 7}}{\text{.3}}$ and $\theta {\text{ = 25}}{{\text{0}}^ \circ }$ , therefore on
substituting the values we get the result as,
${\vec a_x}{\text{ = |}}\vec a|{\text{ }} \times {\text{ cos}}\theta$
$\Rightarrow {\vec a_x}{\text{ = 7}}{\text{.3 }} \times {\text{ cos }}\left( {{\text{25}}{{\text{0}}^ \circ }} \right)$
$\Rightarrow {\vec a_x}{\text{ = 7}}{\text{.3 }} \times {\text{ }}\left( { - 0.34} \right)$
$\Rightarrow {\vec a_x}{\text{ = - 2}}{\text{.482 m}}$

(b) Similarly we can find y component of vector $\vec a$ as,
${\vec a_y}{\text{ = |}}\vec a|{\text{ }} \times {\text{ sin}}\theta$
Here we multiply ${\text{sin}}\theta$ with the magnitude of vector $\vec a$ and we know that according to question, ${\text{|}}\vec a|{\text{ = 7}}{\text{.3}}$ and $\theta {\text{ = 25}}{{\text{0}}^ \circ }$ , therefore on substituting the values we get the result as,
${\vec a_y}{\text{ = |}}\vec a|{\text{ }} \times {\text{ sin}}\theta$
$\Rightarrow {\vec a_y}{\text{ = 7}}{\text{.3 }} \times {\text{ sin }}\left( {{{250}^ \circ }} \right)$
$\Rightarrow {\vec a_y}{\text{ = 7}}{\text{.3 }} \times {\text{ }}\left( { - 0.93} \right)$
$\therefore {\vec a_y}{\text{ = - 6}}{\text{.789 m}}$

Therefore we have calculated the x and y component of a vector called $\vec a$.

Note: The value of sine and cosine of the given angle can be find out with the help of trigonometric tables and we can also convert them in terms of $\pi$ by multiplying the angle with $\dfrac{\pi }{{180}}$. We can also round off these values for easy calculations.The magnitude of a vector is basically the length of a vector in a particular direction, therefore it is measured in meters.