Question

Weight of a body of mass $m$ decreases by 1% when it is raised to a height $h$ above the earth’s surface. If the body is taken to a depth $h$ in a mine, then its weight will
A) decrease by 0.5%
B) decrease by 2%
C) increase by 0.5%
D) increase by 1%

Answer 1

The weight of a body at the surface of the earth is given by the product of its mass and the acceleration due to gravity at the surface. When the body is raised to a height or lowered to a height from the surface of the earth the acceleration due to gravity also changes in accordance with the change in height.

Formula used:
-The acceleration due to gravity at a height above the surface of the earth is given by, $g' = g\left( {1 - \dfrac{{2h}}{R}} \right)$ where $g$ is the acceleration due to gravity at the surface of the earth, $h$ is the height and $R$ is the radius of the earth.
-The acceleration due to gravity at a depth below the surface of the earth is given by, $g' = g\left( {1 - \dfrac{d}{R}} \right)$ where $g$ is the acceleration due to gravity at the surface of the earth, $d$ is the depth and $R$ is the radius of the earth.

Complete step by step solution
Step 1: Sketch a figure describing the body above and below the surface of the earth.

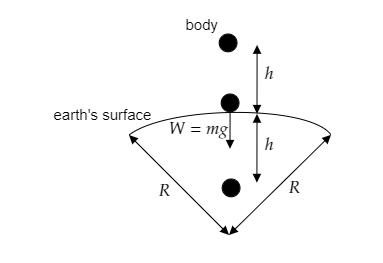
In the above figure, $R$ represents the radius of the earth. The height above the surface of the earth at which the body is placed is given to be $h$ . The body is later placed at an equal depth below the surface of the earth.
The mass of the body is given to be $m$ . In the above figure, $W = mg$ is the weight of the body at the surface of the earth ( $g$ is the acceleration due to gravity at the surface of the earth).
Let ${W_1} = m{g_1}$ be the weight of the body at the height above the surface of the earth where ${g_1}$ is the acceleration due to gravity at the given height above the surface of the earth. It is mentioned that the original weight of the body decreases by 1% when it is raised to the given height. $\Rightarrow {W_1} = 0 \cdot 99W$ -------- (1)
Let ${W_2} = m{g_2}$ be the weight of the body at the height below the surface of the earth. ( ${g_2}$ is the acceleration due to gravity at that depth).
Step 2: Using equation (1) obtain an expression for the height at which the body is placed.
Equation (1) can also be expressed as $m{g_1} = 0 \cdot 99mg$ .
$\Rightarrow {g_1} = 0 \cdot 99g$ or $\dfrac{{{g_1}}}{g} = 0 \cdot 99$ --------- (2)
Now the acceleration due to gravity at the given height $h$ above the surface of the earth can be expressed as ${g_1} = g\left( {1 - \dfrac{{2h}}{R}} \right)$ --------- (3)
Substituting equation (3) in (2) we get, $\dfrac{{g\left( {1 - \dfrac{{2h}}{R}} \right)}}{g} = 0 \cdot 99$
$\Rightarrow \dfrac{{2h}}{R} = 1 - 0 \cdot 99 = 0 \cdot 01$
$\Rightarrow h = \dfrac{{0 \cdot 01R}}{2} = 0 \cdot 005R$
Thus the height at which the body is placed is given by, $h = 0 \cdot 005R$ .
Step 3: Express the acceleration due to gravity at the given depth below the surface to obtain the weight of the body at the depth.
The acceleration due to gravity at the given depth below the surface of the earth can be expressed as ${g_2} = g\left( {1 - \dfrac{h}{R}} \right)$ -------- (4)
Substituting for $h = 0 \cdot 005R$ in equation (4) we get, ${g_2} = g\left( {1 - \dfrac{{0 \cdot 005R}}{R}} \right) = 0 \cdot 995g$
Thus the acceleration due to gravity at the given depth is ${g_2} = 0 \cdot 995g$ .
Now the weight of the body at this depth will be ${W_2} = m{g_2} = 0 \cdot 995mg = 0 \cdot 995W$ .
The percentage of change in the weight of the body at the given depth will be
$\Delta W = \left( {\dfrac{{{W_2} - W}}{W}} \right) \times 100$ --------- (5)
Substituting for ${W_2} = 0 \cdot 995W$ in equation (5) we get, $\Delta W = \left( {\dfrac{{0 \cdot 995W - W}}{W}} \right) \times 100 = - 0 \cdot 05$%
Thus the weight decreases by 0.5%.

So the correct option is A.

Note: For the same height above and below the surface of the earth, the acceleration due to gravity decreases but the decrease is not the same. Here the calculated change in the weight carries a negative sign. This negative sign indicates that the weight decreases. If the change in the weight of the body was obtained to be a positive value we could conclude that the weight increased.