Solveeit Logo
Login

Question

Question: We wish to obtain a capacitance of \[5\mu F\], by using some capacitors, each of \[2\,\mu F\] . Then...

We wish to obtain a capacitance of 5μF5\mu F, by using some capacitors, each of 2 μF2\,\mu F . Then the minimum number of capacitors required is?
A. 3
B. 4
C. 5
D. not possible

Explanation

Solution

We know that capacitors work in an opposite way as compared to resistors when connected in either series or parallel combination. So, we will start by checking the equivalent capacitance of capacitors connected in series and in parallel. We see both conditions do not give equivalent capacitance of 5μF5\mu F. Hence we will combine capacitors in parallel and series and look at the minimum number of capacitors required.

Complete step by step answer:
As mentioned in the hint above the capacitors in series connection is given by :
C(eq)=C1+C2+......+CnC_{(eq)} = C_1 + C_2 + ...... + C_n.............(in parallel)
And ; 1C(eq)=1C1+1C2+......+1C3\dfrac{1}{{C(eq)}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + ...... + \dfrac{1}{{C_3}}......(in series)
The case of series combination we see that: 1C(eq)=12+12\dfrac{1}{{C(eq)}} = \dfrac{1}{2} + \dfrac{1}{2}
1C(eq)=11=1μF\dfrac{1}{{C(eq)}} = \dfrac{1}{1} = 1\mu F
And in case or parallel: C(eq)=2+2=4μFC_{(eq)} = 2 + 2 = 4\mu F
But we need 5μF5\mu F, hence we will try making different combinations. This can be achieved by adding 2 capacitors in series, it will give effective capacitance of 1μF1\mu F.Now if we add 2 capacitors in parallel to the earlier circuit we get effective capacitance as 5μF5\mu F.

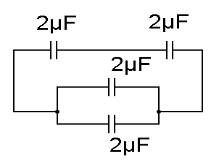
C(eq) because the series is 1microfarad and because of the parallel connection is 4 microfarad. Hence the effective capacitance of circuit =1μF+4μF = 1\mu F + 4\mu F.
C(eq)=5μFC_{(eq)} = 5\mu F
Hence looking at all the observations above we see that to make capacitance of 5μF5\mu F using capacitors of 2μF2\mu F, minimum 4 capacitors will be required.

Hence the correct option is B.

Note: We should remember that capacitors in series is given by 1C(eq)=1C1+1C2+......+1C3\dfrac{1}{{C(eq)}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + ...... + \dfrac{1}{{C_3}} and the capacitor in parallel is given by C(eq)=C1+C2+......+CnC(eq) = C_1 + C_2 + ...... + C_n. It should not be confused with a combination of resistors.Here C(eq) is equivalent capacitance. There can be many other combinations but keep in mind we need a minimum number of capacitors.