Question

We are looking at the oscillating thing hanging from a spring. The system was set vibrating by pulling the thingy down below its equilibrium position and then letting it go from rest. If the initial displacement is doubled then what happens to the maximum kinetic energy of the thing?

Answer 1

As the thingy is let go from rest, it will vibrate about its equilibrium position. The maximum displacement of the thingy to either side of the equilibrium position is referred to as its amplitude. The kinetic energy of the oscillating thingy is proportional to the square of the displacement of the oscillating thingy.

Formula used:
-The kinetic energy of an oscillator is given by, $K = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the oscillator and $v$ is its velocity.

Complete step by step solution:
Step 1: Sketch the given figure and mark the direction of displacement.

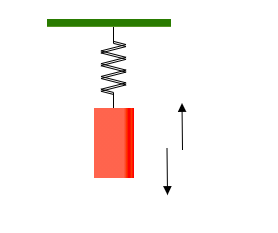
The oscillating thingy will undergo a displacement along the y-direction.
Step 2: Express the kinetic energy of the oscillating thingy.
The given oscillating thingy is said to vibrate about its equilibrium position when released from rest.
Let $m$ be its mass and $v$ be its velocity.
Then the kinetic energy of the oscillating thingy can be expressed as $K = \dfrac{1}{2}m{v^2}$ -------- (1).
Express the dependence of the velocity of the oscillating thingy on its amplitude.
When the displacement becomes maximum, the velocity of the oscillating thingy can be expressed as $v = A\omega$ ------- (2) where $A$ is its maximum displacement or amplitude and $\omega$ is its angular frequency.
Substituting equation (2) in (1) we get, $K = \dfrac{1}{2}m{\omega ^2}{A^2}$
$\Rightarrow K \propto {A^2}$
So when the displacement is doubled i.e., $A \to 2A$ , $K \propto {\left( {2A} \right)^2}$
$\Rightarrow K \propto 4{A^2}$ .

Thus the maximum kinetic energy of the oscillating thingy will increase by a factor of 4.

Note: The kinetic energy of the oscillating thingy will be maximum when the displacement is maximum i.e. when the displacement is equal to the amplitude of the thingy. The angular frequency $\omega$ of the oscillating thing remains constant no matter what its displacement is. So the velocity $v$ of the oscillating thingy will change only when the initial displacement of the thingy changes which will then result in a different amplitude.