Question

Water rises to a height of 2 cm in a capillary tube. if the tube is tilted 60° from the vertical, water will rise in the tube to a length of
A. $4.0cm$
B. $2.0cm$
C. $1.0cm$
D. Water will not rise at all

Answer 1

The rise of water in a capillary tube is governed by the fact that the pressure at the liquid surface outside the capillary tube and the pressure at the same height inside the capillary tube needs to be the same. We will derive from this concept to get the answer.
Formula used:
Trigonometric Relation: $\cos \theta =\dfrac{base}{hypotenuse}$

Complete answer:
The initial capillary condition is given as:

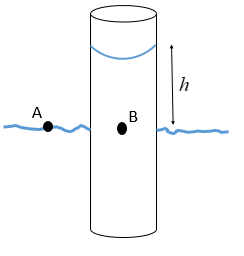
Here, let the pressure at the water surface outside the capillary, i.e. at A, be ${{P}_{0}}$. At the same time the pressure at the same height inside the capillary, i.e. at point B, is not the same.
To make this pressure, at point B, same as that of the pressure at point A, the water inside the capillary tube rises and the excess pressure created, as a result, helps make the pressure at point B same as that at point A.
Also, we know that the excess pressure inside a capillary tube is given by $\dfrac{2T}{R}$.
This principle holds true even when the capillary is tilted. That means that even with the tilted capillary, the vertical rise of the water in the capillary tube is the same as the case when it is not tilted.
This can be understood with the diagram below:

Hence, clearly, we can apply simple maths to find out the length of the water column rise in the capillary $\left( l \right)$.
Here, $\cos ({{60}^{{}^\circ }})=\dfrac{h}{l}$
$\Rightarrow l=\dfrac{h}{\cos (60{}^\circ )}$
$\Rightarrow l=2h$
Also, it is given in the question that the initial rise in the water level was $2cm$
Hence, the rise in water in tilted tube is:
$\Rightarrow l=2\times 2cm$
$\Rightarrow l=4cm$

So, the correct answer is “Option A”.

Note:
The vertical rise in height of water remains the same for any degree of tilt or for no tilt to maintain the same excess pressure. The excess pressure applied by the fluid at a depth of $h$below its surface is given by ${{P}_{excess}}=h\rho g=\dfrac{2T}{R}$. Here, $\rho$is the density of fluid, $T$is the surface tension and $R$is the radius of the meniscus.