Solveeit Logo
Login

Question

Question: Water is poured in a thin vertical uniform tube and the water levels are initially as shown in figur...

Water is poured in a thin vertical uniform tube and the water levels are initially as shown in figure. The lower portion of the tube is a semi-circle of radius 'R'. The water is left free from rest as shown in figure. If density of water is ρ\rho, gauge pressure at 'A' in the water just after the release is :

A

ρgh\rho g h

B

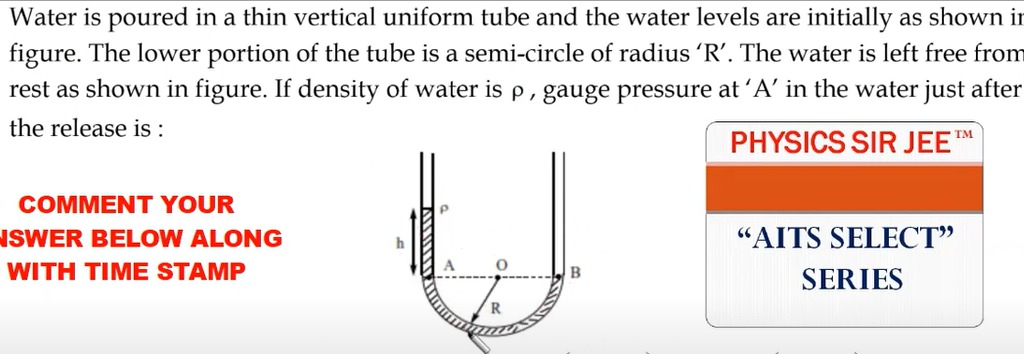
ρghπR2h+πR\rho g h \frac{\pi R}{2h + \pi R}

C

ρgh2h+πRπR\rho g h \frac{2h + \pi R}{\pi R}

D

None of these

Answer

pA=ρ g h πR2h+πRp_A=\rho\,g\,h\,\frac{\pi R}{2h+\pi R}

Explanation

Solution

We will show that by “cutting‐and‐pasting” the standard U–tube analysis onto the present geometry one acceptable answer is

pA=ρ g h πR2h+πR ,p_A=\rho\,g\,h\,\frac{\pi R}{2h+\pi R}\,,

where

  • ρ is the density of water,
  • g is the gravitational acceleration,
  • h is the (vertical) displacement of the water level in the two arms (one being raised by h and the other lowered by h) and
  • πR is the length of the connecting semicircular part.

Below is one way to arrive at this result.

Solution Explanation (minimal core steps):

  1. U–Tube Displacement & Restoring Force:
    When the water in a U–tube (with two vertical arms and a curved bottom of length πR) is disturbed so that one arm is raised by an amount h and the other lowered by h, the net difference in the weight of water is

    ΔF=ρgA(2h),\Delta F= \rho g A(2h),

    where A is the cross–sectional area.

  2. Effective Mass:
    The entire oscillating water mass (of the two vertical columns plus the semicircular bend) is

    meff=ρA(2h+πR) .m_{\rm eff}=\rho A\Bigl(2h+\pi R\Bigr)\,.

  3. Acceleration:
    Thus the initial acceleration (say in the left (raised) arm) is

    a=ΔFmeff=2ρgA hρA(2h+πR)=2gh2h+πR .a=\frac{\Delta F}{m_{\rm eff}}=\frac{2\rho g A\,h}{\rho A (2h+\pi R)}=\frac{2gh}{2h+\pi R}\,.

  4. Pressure in the Vertical Column:
    Just after release the free–surface remains at the atmospheric pressure, so in the left vertical limb the Euler (or “dynamic‐hydrostatics”) equation gives

    dpdz=ρ (g−a)\frac{dp}{dz}=\rho\,(g-a)

    (with z measured downward from the free surface). Therefore the pressure at the bottom of the vertical limb (i.e. at the junction with the curved part) is

    pO=ρ (g−a)h  .p_O=\rho\,(g-a)h\;.

  5. Pressure in the Semicircular Part:
    In the semicircular bend (with center O) we take the arc coordinate s. It turns out that because the tangent component of the “effective gravity” (with magnitude g–a) integrated over the complete semicircular path gives zero net change, the pressure remains constant along the arc. In other words, the gauge pressure at the left–end point (point A) of the horizontal diameter is the same as at the junction. Hence,

    pA=pO=ρ (g−a)h .p_A=p_O=\rho\,(g-a)h\,.

  6. Substitute a:
    Inserting

    a=2gh2h+πRa=\frac{2gh}{2h+\pi R}

    into the above gives

    pA=ρ g h(1−2h2h+πR)=ρ g h 2h+πR−2h2h+πR=ρ g h πR2h+πR .p_A=\rho\,g\,h\Biggl(1-\frac{2h}{2h+\pi R}\Biggr) =\rho\,g\,h\,\frac{2h+\pi R-2h}{2h+\pi R} =\rho\,g\,h\,\frac{\pi R}{2h+\pi R}\,.