Question

Water is flowing in a stream with velocity 5 km/hr in an easterly direction relative to the shore. Speed of a boat relative to still water is 20 km/hr. If the boat enters the stream heading North, with what velocity will the boat actually travel?​

Answer 1

This will be solved by considering various velocity vectors and adding them. Here perpendicular axes are the x axis i.e east direction and the y axis i.e north direction. We get the angle made by the resultant vector with x axis i.e east direction and we can find the magnitude of resultant by vector addition.

Formula used:
$\mathop {{V_{bg}}}\limits^ \to = \mathop {{V_{bw}}}\limits^ \to + \mathop {{V_{wg}}}\limits^ \to$

Complete step by step answer:
This can be solved by using the relative velocity concept. We cannot absolutely tell whether the body is in motion or in rest. It depends on the observer's point of view. If the observer is moving then the body which is at rest with respect to ground will be under motion with respect to the moving observer. So everything is relative. Nothing is absolute.
Here water is moving in east direction with respect to ground and its velocity is given by $\mathop {{V_{wg}}}\limits^ \to$ and velocity of boat with respect to still water in the sense velocity of boat with respect to water and is given by $\mathop {{V_{bw}}}\limits^ \to$ and we are asked to find out the velocity of boat with respect to ground $\mathop {{V_{bg}}}\limits^ \to$. By referring to the below diagram we get the clear idea.

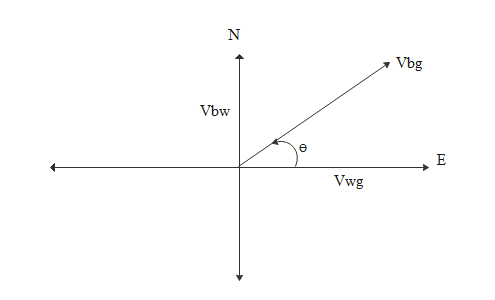
So
$\mathop {{V_{bg}}}\limits^ \to = \mathop {{V_{bw}}}\limits^ \to + \mathop {{V_{wg}}}\limits^ \to$
$\mathop {{V_{bw}}}\limits^ \to = 20\mathop j\limits^ \wedge$ and $\mathop {{V_{wg}}}\limits^ \to = 5\mathop i\limits^ \wedge$
\eqalign{ & \Rightarrow \tan \theta = \dfrac{{20\mathop j\limits^ \wedge }}{{5\mathop i\limits^ \wedge }} \cr & \Rightarrow \theta = {\tan ^{ - 1}}\left( 4 \right) \cr}
The direction of actual velocity of the boat with respect to ground is $\theta = {\tan ^{ - 1}}\left( 4 \right)$ north of east.
The magnitude of velocity of boat with respect to ground is
\eqalign{ & \mathop {{V_{bg}}}\limits^ \to = \mathop {{V_{bw}}}\limits^ \to + \mathop {{V_{wg}}}\limits^ \to \cr & \Rightarrow {V_{bg}} = \sqrt {{V_{bw}}^2 + {V_{wg}}^2} \cr & \Rightarrow {V_{bg}} = \sqrt {{{20}^2} + {5^2}} \cr & \therefore {V_{bg}} = 20.61km/hr \cr}

Note:
Since the boat is trying to go exactly to the north, i.e to the shore, he is trying to cross the river in the shortest time. There are two conditions, one is the shortest time and the shortest path. In the shortest path the horizontal drift will be zero. In the shortest time the drift will not be zero but the time will be minimum.