Question

Water is flowing continuously from a tap having an internal diameter $8 \times {10^{ - 3}}{\text{m}}$ . The water velocity as it leaves the tap is $0 \cdot 4{\text{m}}{{\text{s}}^{ - 1}}$ . Find the approximate diameter of the water stream at a distance $2 \times {10^{ - 1}}{\text{m}}$ below the tap.
A) $5 \cdot 0 \times {10^{ - 3}}{\text{m}}$
B) $7 \cdot 5 \times {10^{ - 3}}{\text{m}}$
C) $9 \cdot 6 \times {10^{ - 3}}{\text{m}}$
D) $3 \cdot 6 \times {10^{ - 3}}{\text{m}}$

Answer 1

The velocity and diameter of the stream of water at the given distance will be different from that at the opening of the tap. The equation of continuity for the flow of liquids suggests that the volume flux of the water stream at the opening of the tap and that at the given distance must be equal. The volume flux is given by the product of the velocity of the water stream and its area. The velocity of the water stream at the given distance can be obtained using Newton’s third equation of motion.

Formulas used:
-Newton’s third equation of motion for a body is given by, ${v^2} - {u^2} = 2as$ where $v$ is the final velocity of the body, $u$ is its initial velocity, $a$ is its acceleration and $s$ is its displacement.

-The equation of continuity for the flow of a liquid is given by, ${A_1}{v_1} = {A_2}{v_2}$ where ${A_1}$ , ${v_1}$ are the area and the velocity of the liquid at one point along the flow and ${A_2}$ , ${v_2}$ are the area and velocity of the liquid at another point along the flow.

Complete step by step solution:
Step 1: Sketch a figure of the water stream for the given distance.

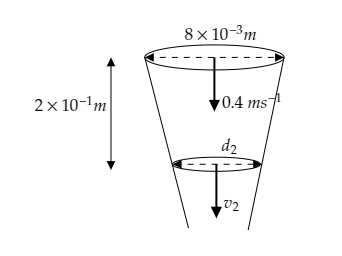
The above figure depicts the stream of water flowing from a tap for the distance $s = 2 \times {10^{ - 1}}{\text{m}}$ below the tap.

The inner diameter of the tap is given to be ${d_1} = 8 \times {10^{ - 3}}{\text{m}}$ and the area of the water stream at the opening of the tap will be ${A_1} = \pi {\left( {\dfrac{{{d_1}}}{2}} \right)^2} = \pi {\left( {\dfrac{{8 \times {{10}^{ - 3}}}}{2}} \right)^2}{{\text{m}}^2}$ .

The velocity of the water at the opening of the tap is given to be ${v_1} = 0 \cdot 4{\text{m}}{{\text{s}}^{ - 1}}$ .

Let ${A_2} = \pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2}$ and ${v_2}$ be respectively the area and velocity of the water stream at the distance $s$ below the tap ( ${d_2}$ is the diameter of the water stream at the given distance).

Step 2: Using Newton’s third equation of motion, obtain the velocity ${v_2}$ of the water stream.

Newton’s third equation of motion for the stream of water at the given distance can be expressed as ${v_2}^2 - {v_1}^2 = 2gs$ --------- (1) ( $g$ is the acceleration due to gravity).

$\Rightarrow {v_2} = \sqrt {2gs + {v_1}^2}$ -------- (2)

Substituting for $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ , $s = 2 \times {10^{ - 1}}{\text{m}}$ and ${v_1} = 0 \cdot 4{\text{m}}{{\text{s}}^{ - 1}}$ in equation (2) we get, ${v_2} = \sqrt {2 \times 10 \times \left( {2 \times {{10}^{ - 1}}} \right) + {{\left( {0 \cdot 4} \right)}^2}} = 2 \cdot 04{\text{m}}{{\text{s}}^{ - 1}}$

Thus the velocity of the water stream at the given distance below the tap is obtained to be ${v_2} = 2 \cdot 04{\text{m}}{{\text{s}}^{ - 1}}$ .

Step 3: Using the continuity equation, obtain the diameter ${d_2}$ of the water stream.
The equation of continuity for the flow of water from the tap can be expressed as

${A_1}{v_1} = {A_2}{v_2}$ -------- (3)

Substituting for ${A_1} = \pi {\left( {\dfrac{{8 \times {{10}^{ - 3}}}}{2}} \right)^2}{{\text{m}}^2}$ , ${A_2} = \pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2}$ , ${v_2} = 2 \cdot 04{\text{m}}{{\text{s}}^{ - 1}}$ and ${v_1} = 0 \cdot 4{\text{m}}{{\text{s}}^{ - 1}}$ in equation (3) we get, $\pi {\left( {\dfrac{{8 \times {{10}^{ - 3}}}}{2}} \right)^2} \times 0 \cdot 4 = \pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2} \times 2 \cdot 04$

Cancelling out the similar terms we get, ${\left( {8 \times {{10}^{ - 3}}} \right)^2} \times 0 \cdot 4 = {d_2}^2 \times 2 \cdot 04$

$\Rightarrow {d_2} = \sqrt {\dfrac{{{{\left( {8 \times {{10}^{ - 3}}} \right)}^2} \times 0 \cdot 4}}{{2 \cdot 04}}} \approx 3 \cdot 6 \times {10^{ - 3}}{\text{m}}$

$\therefore$ the required diameter of the water stream is obtained to be ${d_2} \approx 3 \cdot 6 \times {10^{ - 3}}{\text{m}}$ .

So the correct option is D.

Note: The stream of water flowing from the tap has a conical shape. The velocity of the water stream at the opening of the tap ${v_1}$ will be the initial velocity of the stream and the velocity at the given distance $s$ below the tap will be the final velocity of the water stream. Also, as the water is continuously flowing down from the tap, its acceleration will be the acceleration due to gravity $g$ . These facts are considered while expressing the equation of motion for the water stream (equation (1)).