Question

Water in a river flows from west to east at 4kmph. A man on the north bank capable of swimming at kmph crossed the river in the shortest possible time. In which direction should he swim along?
(A) North
(B) South
(C) ${30^ \circ }$ west of north
(D) ${30^ \circ }$ east of north

Answer 1

Hint : We can solve this question by concepts of relative velocity and components of velocity. The velocity of the man swimming in the river with respect to the velocity of the river is to be examined properly before we decide on the direction in which the man swims.

Formula Used: The formulae used in the solution are given here,
$t = \dfrac{d}{{{v_s}\cos \theta }}$ where $t$ is the time taken to cross the river, $d$ is the depth of the river, $\cos \theta$ is the direction of swimming and ${v_s}$ is the velocity of the swimmer.

Complete step by step answer
If a man is to swim to reach the other bank of the river in the shortest time, he should swim perpendicular to the river flow. This maximizes the velocity of the man, thus minimizing the ratio between the distance and effective velocity. This gives us the minimum time. In the following figure, ${{\text{V}}_{\text{R}}}$ is the velocity of the river and ${{\text{V}}_{\text{s}}}$ is the velocity of the swimmer and $d$ is the depth of the river. It can be understood from the figure that the shortest possible time t should be along AB direction.

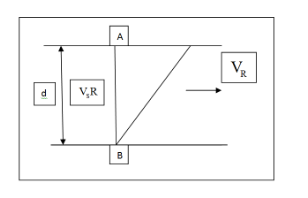
We know that,
$t = \dfrac{d}{{{v_s}\cos \theta }}$ where $t$ is the time taken to cross the river, $d$ is the depth of the river, $\cos \theta$ is the direction of swimming and ${v_s}$ is the velocity of the swimmer.
For $t$ to be minimum the value of $\cos \theta$ must be maximum. The maximum value of $\cos \theta$ is 1, when $\theta = {90^ \circ }$
it is given in the question, the water in the river flows from west to east at 4kmph. For a man, standing in the north direction, the shortest time will be achieved only when $\theta = {90^ \circ }$ .
$\therefore$ The man needs to swim towards the south for minimal time.
The correct answer is Option B.

Note
It is to be remembered here that finding the shortest distance is not the same as finding the shortest time. The shortest time requires maximum effective velocity of the object, the man swimming in this case which minimizes the value of time. We know from our knowledge of mathematics that the shortest possible distance between two points is the perpendicular distance between them. Thus depending on the given values, we can also calculate the shortest distance along with the shortest time.