Question

Water from a tap is emerging vertically downwards with an initial velocity ${{V}_{0}}$. Assume that the pressure is a constant throughout water stream and as it is a steady flow, obtain the distance from the tap at which cross-sectional area of the stream is half of cross-sectional area of stream at the top of the tap:
$\begin{aligned} & A.\dfrac{{{V}_{0}}^{2}}{2g} \\\ & B.\dfrac{3{{V}_{0}}^{2}}{2g} \\\ & C.\dfrac{2{{V}_{0}}^{2}}{g} \\\ & D.\dfrac{5{{V}_{0}}^{2}}{2g} \\\ \end{aligned}$

Answer 1

The velocity equation and continuity equation are used here in order to solve this question. A continuity equation in fluid mechanics is basically an equation that defines the transport of some sort of quantity. It is specifically simple and powerful when we apply it to a conserved quantity, even though it can be generalized to apply to any extensive quantity.
The equation of continuity is given as,
${{A}_{1}}{{V}_{0}}={{A}_{2}}{{V}_{2}}$

Complete step by step answer:

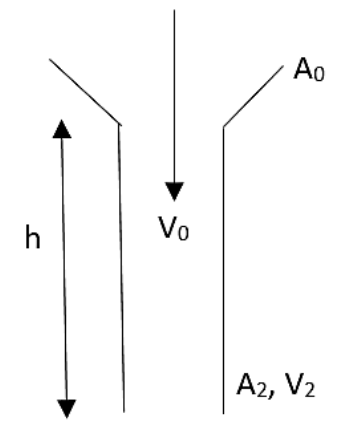
The velocity equation is given as,
${{V}_{2}}^{2}={{V}_{0}}^{2}+2gh$
In which ${{V}_{2}}$ is the velocity with which the flow goes outwards, ${{V}_{0}}$ is the velocity when it is entering, $g$ is the acceleration due to gravity and $h$ is the height of the pipe.
And also the equation of continuity can be written as,
${{A}_{1}}{{V}_{0}}={{A}_{2}}{{V}_{2}}$
Where the ${{A}_{1}}$ area of the pipe at the out is positioned and ${{A}_{2}}$ is the area of the pipe at the entry.
Solving these two equation will give,
$\dfrac{{{A}_{2}}}{{{A}_{1}}}=\dfrac{{{V}_{0}}}{\sqrt{{{V}_{0}}^{2}+2gh}}$
That is,
$\dfrac{{{A}_{2}}}{{{A}_{1}}}=\dfrac{1}{2}=\dfrac{{{V}_{0}}}{\sqrt{{{V}_{0}}^{2}+2gh}}$
Simplifying this will give,
$4{{V}_{0}}^{2}={{V}_{0}}^{2}+2gh$
And then rearranging the terms will give the equation of height of the tube,
That is,
$h=\dfrac{3{{V}_{0}}^{2}}{2g}$

So, the correct answer is “Option B”.

Note: According to the Continuity Equation, if no fluid is being added or removed from a pipe of any length then the mass which is passing across different sections will be the same. This is in accordance with the principle of conservation of mass which states that the matter can neither be created nor be destroyed. The velocity of flow in fluid dynamics is a vector field which is used to mathematically define the motion of a continuum. The length of the flow velocity vector is given as the flow speed and it is a scalar.