Question
Question: Water from a tap emerges vertically downwards with initial velocity \({{4 m/s}}\). The cross-section...
Water from a tap emerges vertically downwards with initial velocity 4m/s. The cross-sectional area of the tap is A. The flow is steady and pressure is constant through the water. The distance hvertically below the tap, where the cross-sectional area will becomes (32)A is: (g=10cm/s2).
Solution
First of all, write the equation of continuity i.e. and then substitute the given value in that equation. Then use Bernoulli’s theorem given as:ρ+ρgh1+21ρv12=ρ+ρgh2+21ρv22and then substitute the values in the formula and solve.
Complete step by step solution:
Equation of continuity
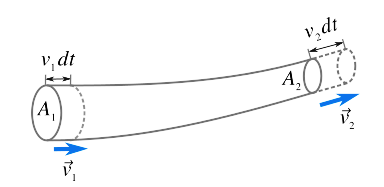
Let us consider a non-viscous, incompressible liquid which is flowing steadily through a pipe. Let A1 be the cross-section, v1 be the fluid velocity, ρ1 be the fluid density at point A(left end of the pipe). And Let A2 be the cross-section, v2 be the fluid velocity, ρ2 be the fluid density at point B(right end of the pipe).
The area of cross-sections are made such that.
Now, formula for mass is given by
And volume can be rewritten as A1>A2 the product of area of cross section and length.
Thus, m=area of cross section×length×density
Therefore, mass of fluid flowing through section A in small time dt is given by
m1=a1v1dtρ1
Similarly, mass of fluid flowing through section B in small time dt is given by
m2=a2v2dtρ2
By conservation of mass,
m1=m2
a1v1dtρ1=a2v2dtρ2
As the fluid is incompressible, so ρ1=ρ2
Hence a1v1=a2v2
On substituting values in above formula, we get
Now using Bernoulli’s theorem
ρ+ρgh1+21ρv12=ρ+ρgh2+21ρv22
On further simplification, we get
g(h1−h2)=21(v22−v12) ⇒g(h)=21(v22−v12)
On substituting values, we get
g(h)=21(62−42) ⇒10×h=21(36−16) ∴h=1m
Thus, the value of h is 1m.
Note: Equation of continuity states that during streamlines flow of the non-viscous and incompressible fluid through pipes of varying cross-section, the product of area of cross-section and the normal fluid velocity remains constant throughout the flow.
