Question

Water flows through a tube as shown in the figure.

The area of cross-section at $A$ and $B$ are $1c{{m}^{3}}$ and $0.5c{{m}^{3}}$ respectively. The height difference between $A$ and $B$ is $5cm$. If the speed of water at $A$ is $10cm{{s}^{-1}}$, find
a) the speed of water at $B$
b) the difference in pressure at $A$ and $B$

Answer 1

Continuity equation for the flow of water suggests that the product of the speed of water and area of the cross-section at $A$ is equal to the product of the speed of water and area of the cross-section at $B$. Bernoulli’s theorem for water flow suggests that pressure difference between $A$ and $B$ is dependent on the difference in speeds of water at $A$ and $B$, the height difference between $A$ and $B$, the density of water, and acceleration due to gravity. From both these equations, the speed of the water at $B$ as well as the pressure difference between $A$ and $B$ can easily be found out.
Formula used:
$\begin{aligned} & 1){{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}} \\\ & 2){{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}} \\\ \end{aligned}$

Complete step-by-step solution
We are provided with the case of water flow in a tube, as shown in the following figure.

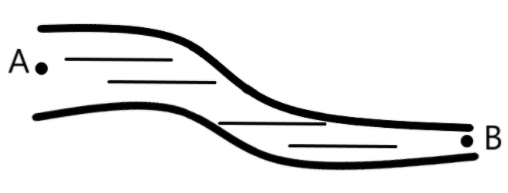
The area of cross-section at $A$ and $B$ are $1c{{m}^{3}}$ and $0.5c{{m}^{3}}$ respectively and the height difference between $A$ and $B$ is $5cm$. If the speed of the water at $A$ is $10cm{{s}^{-1}}$, we are required to find the speed of the water at $B$ and the difference in pressure at $A$ and $B$.
From the continuity equation of water flow, we know that the product of the speed of water and area of the cross-section at $A$ is equal to the product of the speed of water and area of the cross-section at $B$. Mathematically, the equation of continuity is given by
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}$
where
${{A}_{A}}$ is the area of the cross-section at $A$
${{V}_{A}}$ is the speed of the water at $A$
${{A}_{B}}$ is the area of the cross-section at $B$
${{V}_{B}}$ is the speed of the water at $B$
Let this be equation 1.
Substituting the given values from the question in equation 1, we have
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}\Rightarrow 1c{{m}^{3}}\times 10cm{{s}^{-1}}=0.5c{{m}^{3}}\times {{V}_{B}}\Rightarrow {{V}_{B}}=\dfrac{1c{{m}^{3}}\times 10cm{{s}^{-1}}}{0.5c{{m}^{3}}}=20cm{{s}^{-1}}$
where
${{A}_{A}}=1c{{m}^{3}}$ is the area of cross-section at $A$
${{V}_{A}}=10cm{{s}^{-1}}$ is the speed of water at $A$
${{A}_{B}}=0.5c{{m}^{3}}$ is the area of cross-section at $B$
${{V}_{B}}$ is the speed of water at $B$
Let this be equation 2.
Now, we know that Bernoulli’s theorem for water flow suggests that pressure difference between $A$ and $B$ is dependent on the difference in speeds of water at $A$ and $B$, height difference between $A$ and $B$, density of water and acceleration due to gravity. Mathematically, Bernoulli’s theorem can be expressed as
${{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}}\Rightarrow {{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)$
where
${{P}_{A}}$ is the pressure at $A$
${{V}_{A}}$ is the speed of water at $A$
${{P}_{B}}$ is the pressure at $B$
${{V}_{B}}$ is the speed of water at $B$
${{h}_{A}}-{{h}_{B}}$ is the height difference between $A$ and $B$
$\rho$ is the density of water
$g$ is the acceleration due to gravity
Let this be equation 3.
Substituting the values given in the question and equation 2 in equation 3, we have
${{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( {{\left( 10cm{{s}^{-1}} \right)}^{2}}-{{\left( 20cm{{s}^{-1}} \right)}^{2}} \right)+({{10}^{3}}kg{{m}^{-3}})(10m{{s}^{-2}})\left( 5cm \right)$
Simplifying the above expression, we have
${{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( -0.03{{m}^{2}}{{s}^{-2}} \right)+500kg{{m}^{-1}}{{s}^{-2}}=-15kg{{m}^{-1}}{{s}^{-2}}+500kg{{m}^{-1}}{{s}^{-2}}=485Pa$
Let this be equation 4.
Therefore, from equation 2 and equation 4, the speed of the water at $B$ and the pressure difference between $A$ and $B$ are $20cm{{s}^{-1}}$ and $485Pa$.

Note: Students need to be aware of the continuity equation as well as Bernoulli’s theorem for solving this question in no time. They need to be thorough with conversion formulas too. Conversion formulas used in the solution given above are

& 1m={{10}^{2}}cm \\\ & 1cm{{s}^{-1}}={{10}^{-2}}m{{s}^{-1}} \\\ & 1c{{m}^{2}}{{s}^{-2}}={{10}^{-4}}{{m}^{2}}{{s}^{-2}} \\\ & 1Pa=1kg{{m}^{-1}}{{s}^{-2}} \\\ & \\\ \end{aligned}$$ Also, the values of acceleration due to gravity $(g)$ and density of water $(\rho )$ are taken as $10m{{s}^{-2}}$ and $10kg{{m}^{-3}}$, respectively.