Question
Question: Water flows through a horizontal tube of variable cross-section (figure). The area of cross-section ...
Water flows through a horizontal tube of variable cross-section (figure). The area of cross-section at x and y are 40mm2 and 20mm2 ,respectively. If 10cc of water enters per second through x, find (i) the speed of water at x , (ii) the speed of water at y and (iii) the pressure difference Px−Py.
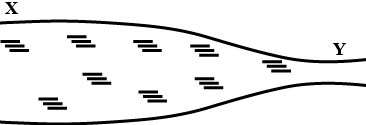
Solution
This question is based on the concept of Bernoulli’s theorem which states that an increase in the speed of a fluid always occurs simultaneously with a decrease in static pressure of the fluid or a decrease in the fluid's potential energy.
Complete step by step answer:
Given,
The area of cross section at x,
a1=40mm2
On converting it into m2, we get,
a1=4×10−5m2
The area of cross section at y,
a2=20mm2
On converting it into m2, we get,
a2=2×10−5m2
The rate of flow of volume =10cc
On converting it into sm3,
The rate of flow of volume =10−5sm3
(a) We know that the volume rate flow,
Q=a1v1
v1=a1Q
v1=4×10−510−5
On further solving, we get,
v1=0.25sm
So, the speed of water at x is v1=0.25sm.
(b) We know that the volume rate flow,
Q=a2v2
v2=a2Q
v2=2×10−510−5
On further solving, we get,
v2=0.5sm
So, the speed of water at y is v2=0.5sm.
(c) According to the Bernoulli’s theorem,
ρPx+2vx2=ρPy+2vy2
On rearranging the above equation,
ρPx−ρPy=2vy2−2vx2
Px−Py=2ρ(vx2−vy2)
On putting the required values, we get,
Px−Py=21000(0.52−0.252)
Px−Py=500(0.52−0.252)
On further solving,
Px−Py=93.8Pa
So, the pressure difference Px−Py is 93.8Pa.
Note: While solving such questions, it is important to note that the rate of flow of water across a section is always equal whether it is a big or a small cross-section. In this question, we have taken the units in the SI system of units, which could also be taken in the CGS system too. The answers will come out the same. If the speed of any fluid increases, this will lead to a decrease in the potential energy of the fluid.
