Question

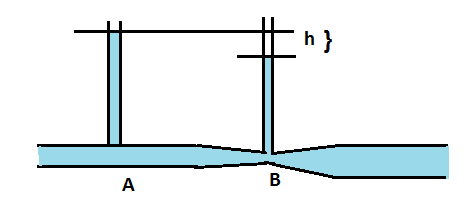
Water flows through a horizontal tube as shown in the figure. If the difference of heights of water column in the vertical columns is h=0.02m, and the areas of cross section at A and B are$4 \times {10^{( - 4)}}{m^2}$and$2 \times {10^{( - 4)}}{m^2}$respectively, then the rate of flow of water across any section is

$$A)130 \times {10^{( - 6)}}{m^3}{s^{( - 1)}} \\\ B)146 \times {10^{( - 6)}}{m^3}{s^{( - 1)}} \\\ C)160 \times {10^{( - 6)}}{m^3}{s^{( - 1)}} \\\ D)170 \times {10^{( - 6)}}{m^3}{s^{( - 1)}} \\\$$

Answer 1

Here, the areas of cross section are given, so we can calculate the relationship between the velocities for both cross sections through the equation of continuity. Then apply the Bernoulli’s principle and put the relationship values for velocities. Then use the formula of flow rate of volume to find the answer.

Complete step by step answer:
Here, let the area of cross section at A be denoted as Aa, while the area of cross section at B be denoted as Ab. Let the velocity at cross section of A be denoted as${v_a}$and the velocity at cross section B be denoted as${v_b}$. Now, the equation of continuity in fluid mechanics suggests that if velocity of a fluid at a cross section is more during a transport, the area of cross section would be less and vice versa. Hence the equation of continuity for the cross sections A and B is as follows:

$$\Rightarrow {A_a}{v_a} = {A_b}{v_b} \\\ \Rightarrow 4 \times {10^{( - 4)}}{v_a} = 2 \times {10^{( - 4)}}{v_b} \\\ \Rightarrow 2{v_a} = {v_b} \\\$$

Thus we obtain the relationship of the velocities at cross section of A and B as above.
Now we use the Bernoulli’s equation, which actually is just another form of the principle of conservation of energy for ideal fluids for a steady or streamline flow of fluid, and it is written as follows for the points A and B:
${P_a} + \rho g{h_a} + \dfrac{1}{2}\rho {v_a}^2 = {P_b} + \rho g{h_b} + \dfrac{1}{2}\rho {v_b}^2$
Here, Pa and Pb are pressure at points A and B, while$\rho$is the density of fluid.
Now, the pipe is actually horizontal and thus,

$$\mathrel\backepsilon {P_a} + \dfrac{1}{2}\rho {v_a}^2 = {P_b} + \dfrac{1}{2}\rho {v_b}^2 \\\ \Rightarrow {P_a} - {P_b} = \dfrac{1}{2}({v_b}^2 - {v_a}^2) \\\ \Rightarrow {P_a} - {P_b} = \dfrac{1}{2}\rho \left( {v_B^2 - v_A^2} \right) = \dfrac{1}{2} \times 1 \times \left( {4v_A^2 - v_A^2} \right) \\\ \Rightarrow 2x1 \times 1000 = 12 \times 1 \times 3{v_a}^2 \\\$$

Pa = Pb= 2cm of water column =2×1×1000$\dfrac{{dyne}}{{c{m^2}}}$
Thus the velocity at A can be given as
${v_a} = \sqrt {\dfrac{{4000}}{3}} = 36.51\dfrac{{cm}}{s}$
Now, the rate of flow of a fluid is given by the volume passed from the cross section per time and it is given in terms of area and velocity for cross section of A as follows:
$\therefore {{V}_{a}}={{A}_{a}}{{v}_{a}}=4\times {{10}^{(-4)}}\centerdot 36.51\times {{10}^{(-2)}} \\\$
$\therefore {{V}_{a}}=146\times {{10}^{(-6)}}\dfrac{{{m}^{3}}}{s} \\\$

So, the correct answer is “Option B”.

Note:
Here, if you calculate the flow rate of the fluid through cross section B, it would still turn out to be the same as flow rate at cross section A as the equation of continuity holds true. Equation of continuity is similar to the law of conservation of momentum, while Bernoulli’s equation is derived from the law of conservation of energy.