Question

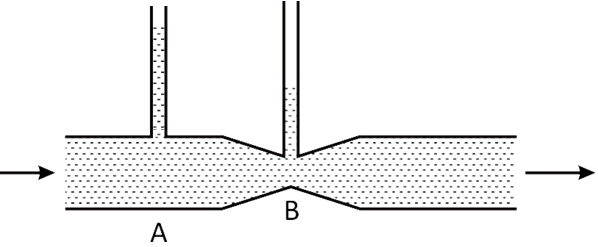
Water flows through a horizontal tube as shown in the figure. If the difference of heights of water column in the vertical tubes is $2\,{\text{cm}}$ , and the areas of cross-section at ${\text{A}}$ and ${\text{B}}$ are $4\,{\text{c}}{{\text{m}}^{\text{2}}}$ and $2\,{\text{c}}{{\text{m}}^{\text{2}}}$ respectively, find the rate of flow of water across any section.

Answer 1

First of all, we will use the equation of continuity to find the relation between the velocities at the two cross-sections. After that we will use Bernoulli's equation to find the difference in pressure. As we also know the difference in heights of the water column, we can calculate the difference in pressure from there too. We will manipulate the required equations accordingly and obtain the result.

Complete step by step answer:
In the given question, we are supplied with the following data:
The difference of heights of the water column in the vertical tubes is $2\,{\text{cm}}$ .
There are two cross-sections selected for the study ${\text{A}}$ and ${\text{B}}$ .
The area of cross section of ${\text{A}}$ is $4\,{\text{c}}{{\text{m}}^{\text{2}}}$ .
The area of cross section of ${\text{B}}$ is $2\,{\text{c}}{{\text{m}}^{\text{2}}}$ .
We are asked to find the rate of flow of water across any section.

To begin with, we will use the equation of continuity for the two cross-sections, which is given by:
${v_{\text{A}}}{a_{\text{A}}} = {v_{\text{B}}}{a_{\text{B}}}$ …… (1)
Where,
${v_{\text{A}}}$ indicates the velocity of the water through the section ${\text{A}}$ .
${a_{\text{A}}}$ indicates the area of the cross section of the section ${\text{A}}$ .
${v_{\text{B}}}$ indicates the velocity of the water through the section ${\text{B}}$ .
${a_{{\text{B - }}}}$ indicates the area of the cross section of the section ${\text{B}}$ .

Substituting the required values in the equation (1) and we get:
{v_{\text{A}}}{a_{\text{A}}} = {v_{\text{B}}}{a_{\text{B}}} \\\ \Rightarrow {v_{\text{A}}} \times 4 = {v_{\text{B}}} \times 2 \\\ \Rightarrow {v_{\text{B}}} = 2{v_{\text{A}}} \\\

Now, we will apply Bernoulli's equation and we will get the following:
$\dfrac{1}{2}\rho v_{\text{A}}^2 + \rho g{h_{\text{A}}} + {p_{\text{A}}} = \dfrac{1}{2}\rho v_{\text{B}}^2 + \rho g{h_{\text{B}}} + {p_{\text{B}}}$ …… (2)
Where,
$\rho$ indicates the density of water.
${h_{\text{A}}}$ indicates the height of the column of section ${\text{A}}$ .
${p_{\text{A}}}$ indicates the pressure of water at the section ${\text{A}}$ .
${h_{\text{B}}}$ indicates the height of the column of section ${\text{B}}$ .
${p_{\text{B}}}$ indicates the pressure of water at the section ${\text{B}}$ .

We know, we will get the same potential energies as the height of both the points is same, then the equation (2) becomes:
\dfrac{1}{2}\rho v_{\text{A}}^2 + {p_{\text{A}}} = \dfrac{1}{2}\rho v_{\text{B}}^2 + {p_{\text{B}}} \\\ \Rightarrow {p_{\text{A}}} - {p_{\text{B}}} = \dfrac{1}{2}\rho v_{\text{B}}^2 - \dfrac{1}{2}\rho v_{\text{A}}^2 \\\
$\Rightarrow {p_{\text{A}}} - {p_{\text{B}}} = \dfrac{1}{2}\rho \left( {v_{\text{B}}^2 - v_{\text{A}}^2} \right)$ …… (3)
We will substitute the required values in the equation (3) and we get:
\Rightarrow {p_{\text{A}}} - {p_{\text{B}}} = \dfrac{1}{2}\rho \left( {v_{\text{B}}^2 - v_{\text{A}}^2} \right) \\\ \Rightarrow {p_{\text{A}}} - {p_{\text{B}}} = \dfrac{1}{2} \times 1 \times \left( {{{\left( {2{v_{\text{A}}}} \right)}^2} - v_{\text{A}}^2} \right) \\\ \Rightarrow {p_{\text{A}}} - {p_{\text{B}}} = \dfrac{{\left( {4v_{\text{A}}^2 - v_{\text{A}}^2} \right)}}{2} \\\
Again, we know,
${p_{\text{A}}} - {p_{\text{B}}}$ is the difference in pressure of the water column, which can be written as:
${p_{\text{A}}} - {p_{\text{B}}} = 0.02\,{\text{m}}$ of water column.
${p_{\text{A}}} - {p_{\text{B}}} = 2 \times 1 \times 1000\,{\text{dyne}}\,{\text{c}}{{\text{m}}^{ - 2}}$

Now, we can write:
{p_{\text{A}}} - {p_{\text{B}}} = \dfrac{{\left( {4v_{\text{A}}^2 - v_{\text{A}}^2} \right)}}{2} \\\ \Rightarrow 2 \times 1 \times 1000 = \dfrac{{3v_{\text{A}}^2}}{2} \\\ \Rightarrow v_{\text{A}}^2 = \dfrac{{4000}}{3} \\\ \Rightarrow {v_{\text{A}}} = \sqrt {\dfrac{{4000}}{3}} \\\
$\Rightarrow {v_{\text{A}}} = 36.51\,{\text{cm}}\,{{\text{s}}^{ - 1}}$

Hence, the rate of flow is:
{v_{\text{A}}}{a_{\text{A}}} \\\ = 36.51\,{\text{cm}}\,{{\text{s}}^{ - 1}} \times 4\,{\text{c}}{{\text{m}}^2} \\\ = 146\,{\text{c}}{{\text{m}}^3}\,{{\text{s}}^{ - 1}} \\\

Note:
While solving this problem, always remember that the rate of flow of water across any section is equal whether it is a bigger or smaller cross-section. We have taken the units in the C.G.S system of units, which you can take in the S.I system too. Answers will come out the same. It is important to note that if the speed of the fluid increases then the fluid’s potential energy decreases.