Question

Volume of HCP unit cell is:
A)$\text{ }24\sqrt{2}\text{ }{{\text{r}}^{3}}$
B)$\text{ }8\sqrt{2}\text{ }{{\text{r}}^{3}}$
C)$\text{ }16\sqrt{2}\text{ }{{\text{r}}^{3}}$
D)$\text{ 24}\sqrt{\text{3}}\text{ }{{\text{r}}^{\text{3}}}$

Answer 1

The volume of the unit cell can be determined by taking the product of the area and height of the cell. For the hexagonal close packing structure$(\text{HCP)}$, the volume is equal to:
$\text{Area of base }\\!\\!\times\\!\\!\text{ Height of the unit cell}$.
Since the base of the hexagonal structure is a hexagon which is itself made of the six equilateral triangles, and the area of the equilateral triangle is$\text{ }\dfrac{\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}$.

Complete step by step answer:
In the hexagonal close packing structure $(\text{HCP)}$ , there are 6 atoms at the corner and in the top layer and bottom layer of the $(\text{HCP)}$structure. There are a total of 12 atoms, 2 atoms at the base centred, and 3 atoms within the $(\text{HCP)}$unit cell.
Each atom at the corner contribute $\text{ }\dfrac{1}{6}\text{ }$ since there are 12 atoms at the corner, therefore the total number of atoms per unit cell is :$\text{ }\dfrac{1}{6}\times 12\text{ = 2}$
Each base entered atoms have a total contribution of $\text{ }\dfrac{1}{2}\text{ }$ , the number of base-centred per unit cell is $\dfrac{1}{2}\times 2\text{ = 1}$
The three atoms within the unit cell give the complete contribution.
Therefore, the contribution of atom in the hexagonal packed structure is calculated as;
$\text{ Number of atom per unit cell of HCP}=\text{ 2 + 1 + 3 = 6 }$

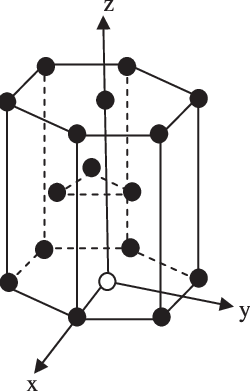
We know that the volume of the unit cell can be represented as the product of the area of base and height of the unit cell.
$\text{Volume of unit cell = Area of base }\\!\\!\times\\!\\!\text{ Height of the unit cell}$
The $(\text{HCP)}$is a hexagonal prism structure. The base of $(\text{HCP)}$is a hexagon. We know that the hexagon is made of the 6 equilateral triangles.
$\text{ Area of equilateral triangle = }\dfrac{\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}$
Therefore, the area of the base is given as,
$\text{ Area of base = 6 }\times \dfrac{\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}$
Let’s the ‘h’ be the height of the hexagonal unit.
Therefore we have,
$\dfrac{\text{h}}{\text{a}}=\sqrt{\dfrac{8}{3}}$
Now, substitute these values in the volume of $(\text{HCP)}$we have,

& \text{Volume of HCP = Area of base }\times \text{ height of the} \\\ & \therefore \text{Volume of HCP = 6 }\times \dfrac{\sqrt{3}}{4}{{\text{a}}^{\text{2}}}\text{ }\times \text{ }\sqrt{\dfrac{8}{3}}\text{ a} \\\ \end{aligned}$$ We know that the edge length ‘a’ is equal to twice the radius of the atom. That is, $\text{a = 2r}$ Substitute these values in the volume we get, $$\text{Volume of HCP = 6 }\times \dfrac{\sqrt{3}}{4}{{\text{a}}^{\text{2}}}\text{ }\times \text{ }\sqrt{\dfrac{8}{3}}\text{ a = 6 }\times \dfrac{\sqrt{3}}{4}{{\text{(2r)}}^{\text{2}}}\text{ }\times \text{ }\dfrac{\sqrt{8}}{\sqrt{3}}\text{ 2r}=\text{24}\sqrt{2}\text{ }{{\text{r}}^{\text{3}}}$$ Therefore, the volume of the hexagonal close packing structure is $$\text{24}\sqrt{2}\text{ }{{\text{r}}^{\text{3}}}$$ **Hence, (A) is the correct option.** **Note:** We can further calculate the Atom packing efficiency of the HCP unit cell by taking the ratio of the volume of atoms in the unit cell to the volume of the unit cell. Here a total of 6 atoms per unit cell. Since atoms are sphere the APF can be calculated as follows, $$$$ $$\text{APF = }\dfrac{\text{Volume of atoms in unit cell}}{\text{Volume of unit cell}}\text{ = }\dfrac{\text{6 }\\!\\!\times\\!\\!\text{ }\dfrac{\text{4}}{\text{3}}\text{ }\\!\\!\pi\\!\\!\text{ }{{\text{r}}^{\text{3}}}}{\text{24}\sqrt{\text{2}}\text{ }{{\text{r}}^{\text{3}}}}\text{ }=\text{ }\dfrac{1}{\text{3}}\text{ }\\!\\!\times\\!\\!\text{ }\dfrac{\text{ }\\!\\!\pi\\!\\!\text{ }}{\sqrt{\text{2}}}\text{ }=\text{ }\dfrac{\text{ }\\!\\!\pi\\!\\!\text{ }}{\text{3}\sqrt{\text{2}}}\text{ }=0.74$$ Therefore, the atomic packing fraction for HCP is equal to the 0.74.