Question

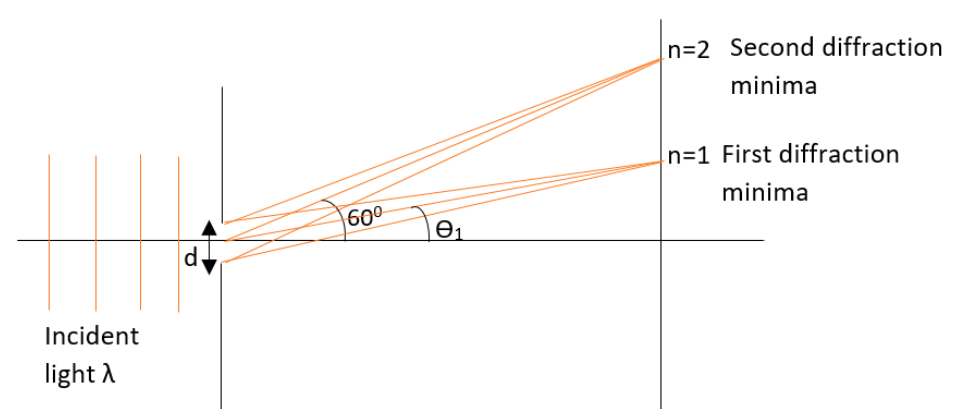
Visible light of wavelength $6000\times {{10}^{-8}}cm$ falls normally on a single slit and develops a diffraction pattern. It is found that the second diffraction minimum is at $60{}^\circ$ from the central maximum. If the first minimum is created at ${{\theta }_{1}}$,​ then ${{\theta }_{1}}$ will be close to?

Answer 1

For the diffraction minima to occur, the product of the order of the patterns formation and the wavelength of the light will be equal to the product of slit width and the sine of the angle at which first minimum is produced. Using this relation, find the slit width of the arrangement for the second minimum. Similarly find the angle for the first diffraction also. These all may help you to solve this question.

Complete step by step answer:
For a diffraction minima to occur, the product of the order of the patterns formation and the wavelength of the light will be equal to the product of slit width and the sine of the angle at which first minimum is produced. That is, we can write that,
$n\lambda =d\sin \theta$
Where $d$ be the slit width, $\lambda$be the wavelength of the light, $\theta$ be the angle of diffraction minimum and $n$ be the order of the minima.
Here it has been mentioned that the wavelength of the light used is,
$\lambda =6000\times {{10}^{-8}}cm$
Therefore for the first condition,
The second diffraction minima has been produced. Hence we can write that,
$n=2$
And the angle between the central maxima and the second diffraction minima will be,
$\theta =60{}^\circ$
Substituting this in the equation,
$\begin{aligned} & 2\lambda =d\sin 60{}^\circ \\\ & d=\dfrac{2\lambda }{\sin 60{}^\circ }=\dfrac{4\lambda }{\sqrt{3}} \\\ \end{aligned}$
Therefore the slit width has been obtained.
Now in the second condition,
The first minima has been produced,
$n=1$
Substituting the values accordingly in the equation will give,
$\begin{aligned} & 1\lambda =d\sin {{\theta }_{1}} \\\ & \sin {{\theta }_{1}}=\dfrac{\lambda }{d} \\\ \end{aligned}$
Now let us substitute the values of slit width in it.
$\sin {{\theta }_{1}}=\dfrac{\lambda }{\dfrac{4\lambda }{\sqrt{3}}}=\dfrac{\sqrt{3}}{4}$
From this the angle will be,
${{\theta }_{1}}={{\sin }^{-1}}\dfrac{\sqrt{3}}{4}\approx 25{}^\circ$

Note: In the single-slit diffraction, the bending phenomenon of light or diffraction occurs that causes light from a coherent source to interfere with itself and develops a distinctive pattern on the screen. This pattern is called a diffraction pattern. There will be minima and maxima in the pattern. Maxima is the portion of higher intensity and minima is the portion of smaller intensity.