Question
Question: (vii) Which formula co-relates degree of dissociation and concentration of electrolyte?...
(vii) Which formula co-relates degree of dissociation and concentration of electrolyte?
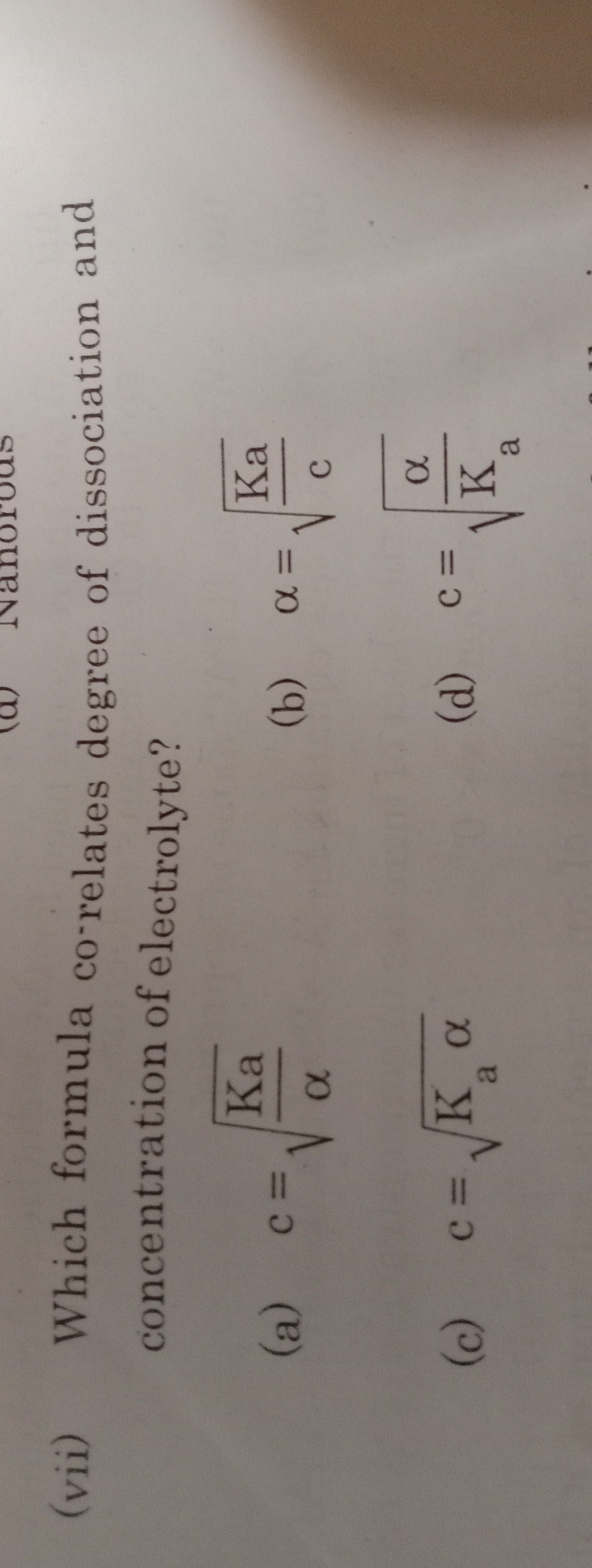
c=αKa
α=cKa
c=Kaα
c=Kaα
α=cKa
Solution
The relationship between the degree of dissociation (α), concentration of the electrolyte (c), and the dissociation constant (Ka) is derived from the equilibrium expression for a weak electrolyte.
Consider a weak acid, HA, dissociating in water:
HA⇌H++A−
Initial concentrations:
c00
At equilibrium:
c(1−α)cαcα
The acid dissociation constant, Ka, is given by:
Ka=[HA][H+][A−]
Substitute the equilibrium concentrations:
Ka=c(1−α)(cα)(cα)
Ka=c(1−α)c2α2
Ka=1−αcα2
For weak electrolytes, the degree of dissociation (α) is very small (i.e., α<<1). Therefore, (1−α) can be approximated as 1.
So, the equation simplifies to:
Ka≈cα2
Rearranging this equation to solve for α:
α2=cKa
Taking the square root of both sides:
α=cKa
