Question
Question: $\int_{0}^{\frac{7}{2}} \sqrt{x+\frac{1}{\sqrt{x+\frac{1}{x+...}}}} dx$....
∫027x+x+x+...11dx.
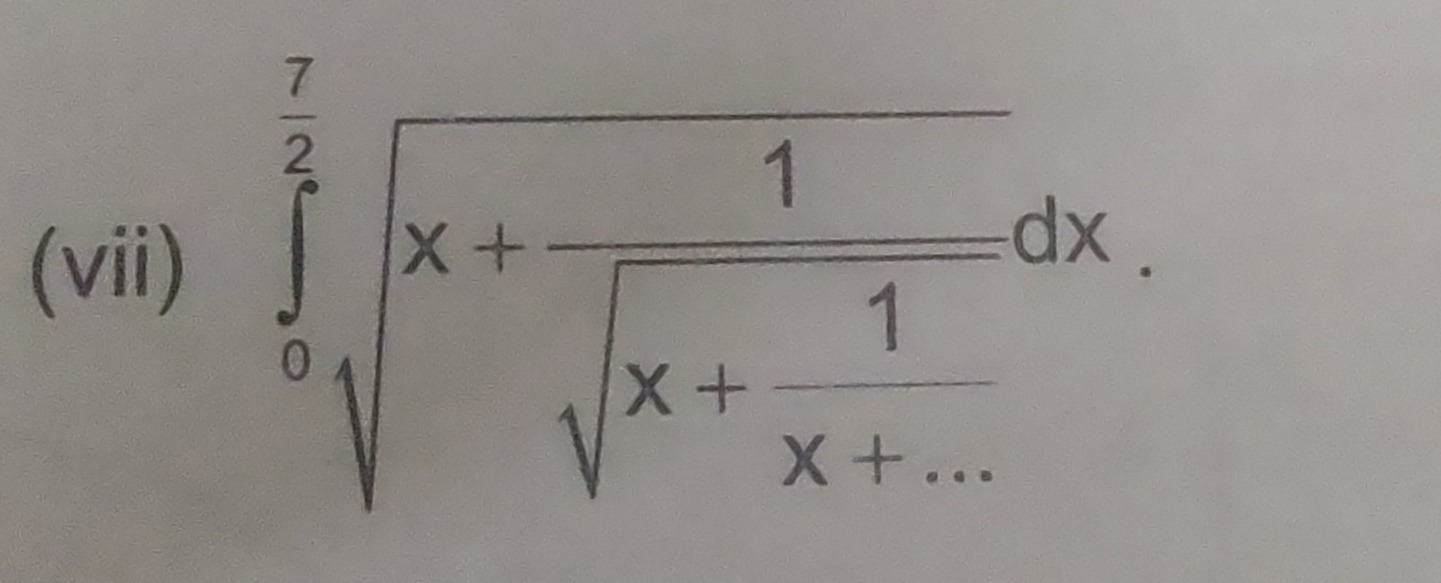
314+ln2
Solution
To evaluate the integral ∫027x+x+x+...11dx, we first simplify the expression inside the integral.
Let y=x+x+x+...11.
This expression can be written recursively as y=x+y1.
Now, we solve for y in terms of x:
Square both sides: y2=x+y1
Multiply by y (since y=…, y must be positive, so y=0):
y3=xy+1
Rearrange the terms to express x in terms of y:
xy=y3−1
x=yy3−1
x=y2−y1
Now we perform a change of variables for the integral from x to y.
First, find dx in terms of dy:
dx=dyd(y2−y1)dy
dx=(2y−(−y21))dy
dx=(2y+y21)dy
Next, change the limits of integration from x to y:
-
Lower limit: When x=0.
Substitute x=0 into x=y2−y1:
0=y2−y1
0=yy3−1
Since y=0, we must have y3−1=0.
y3=1. Since y must be positive, y=1. -
Upper limit: When x=27.
Substitute x=27 into x=y2−y1:
27=y2−y1
27=yy3−1
7y=2(y3−1)
2y3−7y−2=0
We look for positive integer roots. Let P(y)=2y3−7y−2.
Test y=1: P(1)=2(1)3−7(1)−2=2−7−2=−7=0.
Test y=2: P(2)=2(2)3−7(2)−2=2(8)−14−2=16−14−2=0.
So, y=2 is a root. Since x(y)=y2−1/y is an increasing function for y>0 (x′(y)=2y+1/y2>0), y=2 is the correct upper limit.
Now substitute y for the integrand and dx into the integral, with the new limits:
∫027x+x+x+...11dx=∫x=0x=27ydx
=∫y=1y=2y(2y+y21)dy
=∫12(2y2+y2y)dy
=∫12(2y2+y1)dy
Finally, evaluate the definite integral:
=[23y3+ln∣y∣]12
=(2323+ln(2))−(2313+ln(1))
=(316+ln(2))−(32+0)
=316−32+ln(2)
=314+ln(2)
