Question

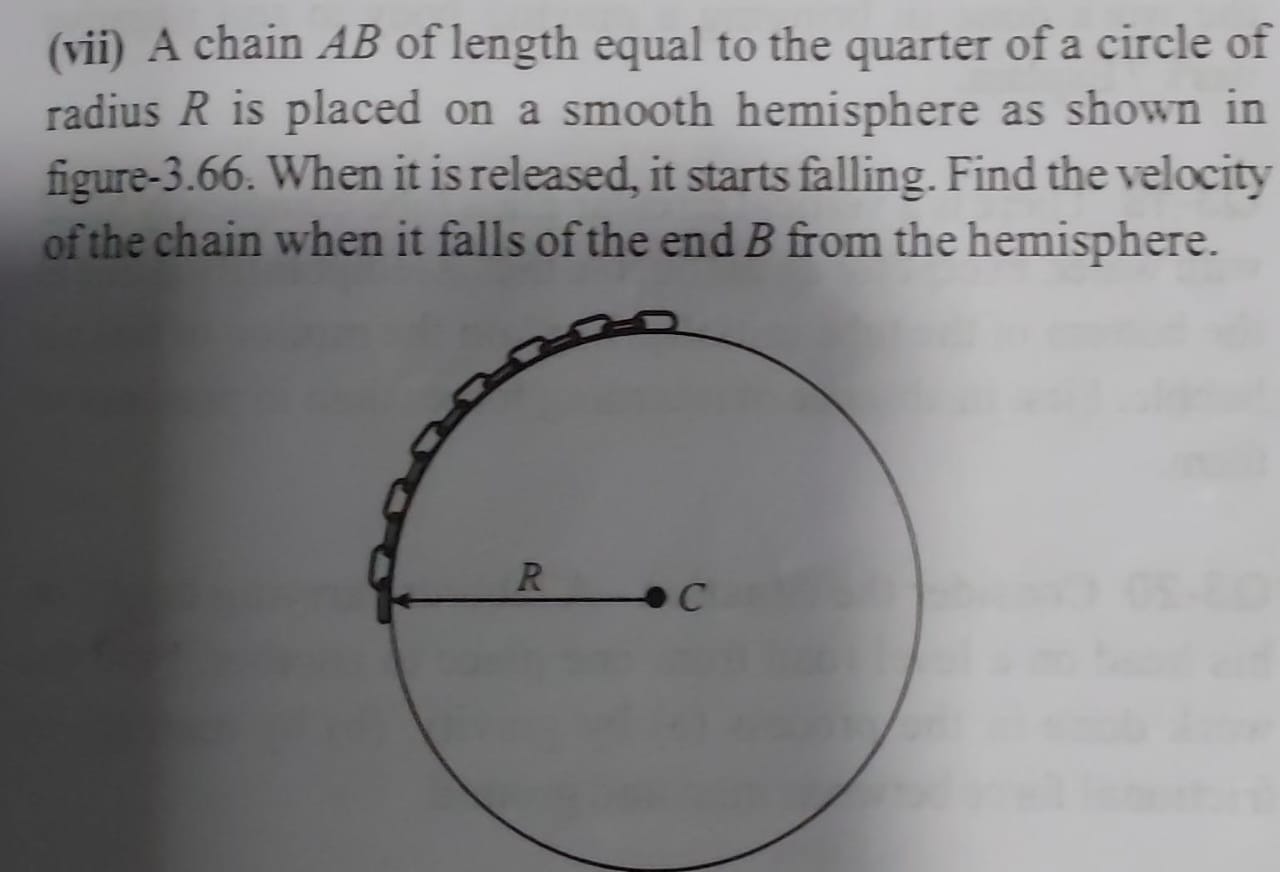
A chain $AB$ of length equal to the quarter of a circle of radius $R$ is placed on a smooth hemisphere as shown in figure-3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end $B$ from the hemisphere.

Answer 1

$2\sqrt{\frac{gR}{\pi}}$

Answer 2

The problem can be solved using the principle of conservation of mechanical energy, as the hemisphere is smooth. Let the total mass of the chain be $M$ and its length be $L$. Given that the length of the chain is a quarter of a circle of radius $R$, we have $L = \frac{1}{4}(2\pi R) = \frac{\pi R}{2}$.

We choose the horizontal plane passing through the center of the hemisphere ($C$) as the reference level for potential energy ($h=0$). Let $\theta$ be the angle measured from the vertical axis passing through $C$. The height of an element of the chain at angle $\theta$ is $h = R\cos\theta$.

The linear mass density of the chain is $\lambda = \frac{M}{L} = \frac{M}{\pi R/2} = \frac{2M}{\pi R}$. A small element of the chain of length $dl = R d\theta$ has mass $dm = \lambda dl = \frac{2M}{\pi R} R d\theta = \frac{2M}{\pi} d\theta$.

Initial State: The chain is placed on the hemisphere. The figure shows the chain starting from the top of the hemisphere (zenith, $\theta=0$) and extending along the arc to point $B$, which is at an angle $\theta = \pi/2$ from the zenith. Thus, the chain covers the angular range from $\theta=0$ to $\theta=\pi/2$. The chain is released from rest, so its initial kinetic energy $K_i = 0$. The initial potential energy $U_i$ is calculated by integrating the potential energy of each element: $U_i = \int_{0}^{\pi/2} dm \cdot g \cdot h = \int_{0}^{\pi/2} \left(\frac{2M}{\pi} d\theta\right) g (R\cos\theta)$ $U_i = \frac{2MgR}{\pi} \int_{0}^{\pi/2} \cos\theta d\theta = \frac{2MgR}{\pi} [\sin\theta]_{0}^{\pi/2}$ $U_i = \frac{2MgR}{\pi} (\sin(\pi/2) - \sin(0)) = \frac{2MgR}{\pi} (1 - 0) = \frac{2MgR}{\pi}$.

Final State: The problem asks for the velocity of the chain when it falls off the end $B$ from the hemisphere. This implies that the entire chain has detached from the hemisphere. We assume that at this point, the entire chain has fallen to the reference level ($h=0$). Therefore, the final potential energy $U_f = 0$. The final kinetic energy of the chain is $K_f = \frac{1}{2} M v^2$, where $v$ is the velocity of the chain.

Conservation of Mechanical Energy: $K_i + U_i = K_f + U_f$ $0 + \frac{2MgR}{\pi} = \frac{1}{2} M v^2 + 0$ $\frac{1}{2} M v^2 = \frac{2MgR}{\pi}$ $v^2 = \frac{4gR}{\pi}$ $v = \sqrt{\frac{4gR}{\pi}} = 2\sqrt{\frac{gR}{\pi}}$.