Question

Which is parallel to $4x+y+1=0$ for the parabola $x^2 = -2y$?

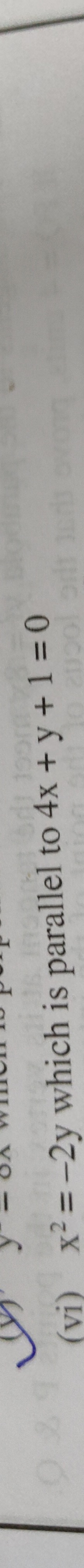
• A. The equation of the tangent line to the parabola $x^2 = -2y$ which is parallel to the line $4x+y+1=0$ is $4x + y - 8 = 0$.
• B. The point of tangency for the parabola $x^2 = -2y$ and a tangent parallel to $4x+y+1=0$ is $(4, -8)$.
• C. The vertex of the parabola $x^2 = -2y$ is $(0, 0)$ and it opens downwards.
• D. The slope of the line $4x+y+1=0$ is $4$.

Answer 1

Answer: (A)

The equation of the tangent line to the parabola $x^2 = -2y$ which is parallel to the line $4x+y+1=0$ is $4x + y - 8 = 0$.

Answer 2

The parabola is given by $x^2 = -2y$, which is in the form $x^2 = -4ay$. Comparing, we get $-4a = -2$, so $a = \frac{1}{2}$. The given line is $4x+y+1=0$. Rewriting in slope-intercept form, $y = -4x - 1$. The slope of this line is $m = -4$. We are looking for a tangent to the parabola that is parallel to this line, so the tangent must also have a slope of $m = -4$. The general equation of a tangent to the parabola $x^2 = -4ay$ with slope $m$ is $y = mx + am^2$. Substituting $a = \frac{1}{2}$ and $m = -4$: $y = (-4)x + \left(\frac{1}{2}\right)(-4)^2 = -4x + \frac{1}{2}(16) = -4x + 8$. Rearranging this into the form $Ax+By+C=0$, we get $4x + y - 8 = 0$.