Question
Question: If $x^y = e^{x-y}$, then show that $\frac{dy}{dx} = \frac{log x}{(1+log x)^2}$...
If xy=ex−y, then show that dxdy=(1+logx)2logx
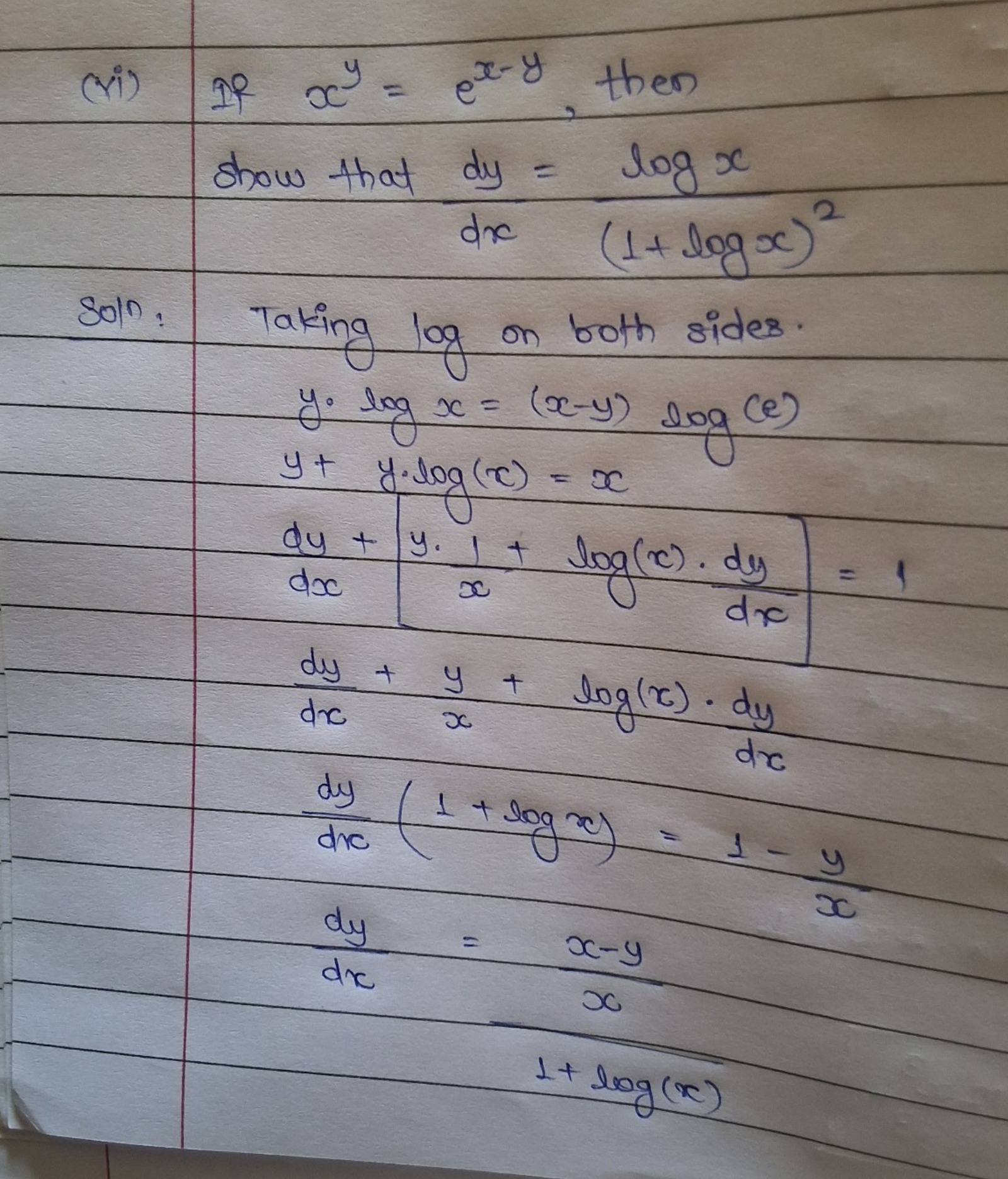
Answer
(1+lnx)2lnx
Explanation
Solution
Solution:
Given
xy=ex−y.Taking natural logarithms on both sides,
ln(xy)=ln(ex−y)⟹ylnx=x−y.Rearrange:
ylnx+y=x⟹y(1+lnx)=x⟹y=1+lnxx.Differentiate using the quotient rule with u=x and v=1+lnx (so that u′=1 and v′=x1):
dxdy=v2u′v−uv′=(1+lnx)21⋅(1+lnx)−x⋅x1=(1+lnx)21+lnx−1=(1+lnx)2lnx.Explanation (Core):
- Take ln on both sides: ylnx=x−y.
- Solve for y: y=1+lnxx.
- Differentiate using the quotient rule to get dxdy=(1+lnx)2lnx.
