Question

Vertical displacement of a plank with a body of mass m on it is varying according to the law $y=\sin \omega t+\sqrt{3}\cos \omega t$. The minimum value of $\omega$for which the mass just breaks off the plank and the moment it occurs first time t=0, are given by
$\begin{aligned} & a)\sqrt{g/2},\dfrac{\sqrt{2}}{6}\dfrac{\pi }{\sqrt{g}} \\\ & b)\dfrac{g}{\sqrt{2}},\dfrac{2}{3}\sqrt{\pi /g} \\\ & c)\sqrt{g/2},\dfrac{\pi }{3}\sqrt{2/g} \\\ & d)\sqrt{2g},\sqrt{2\pi /3g} \\\ \end{aligned}$

Answer 1

It is given in the question that the body of mass m just breaks off the plank at different instant of time. Hence we can say that there exists a restoring force on the body due to the plank. Hence we will first obtain the free body diagram of the above scenario and accordingly obtain the minimum value of $\omega$.

Formula used:
${{F}_{\operatorname{REST}}}=m{{\omega }^{2}}y$
$mg-N=ma$
$y=A\sin (\omega t+\phi )$
$a={{\omega }^{2}}y$

Complete answer:
To begin with first let us analyze the equation of motion of the plank with mass m.
$y=\sin \omega t+\sqrt{3}\cos \omega t$
Let us divide and multiply the above equation by 2. Therefore we get,
$\begin{aligned} & y=\sin \omega t+\sqrt{3}\cos \omega t \\\ & \Rightarrow y=2\left[ \dfrac{1}{2}\sin \omega t+\dfrac{\sqrt{3}}{2}\cos \omega t \right]\text{, }\because \sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}and\cos {{60}^{\circ }}=\dfrac{1}{2} \\\ & \Rightarrow y=2\left[ \cos {{60}^{\circ }}sin\omega t+\sin {{60}^{\circ }}\cos \omega t \right]\text{, }\because \operatorname{cosBsinA}+\operatorname{sinB}\operatorname{cosA}=Sin(A+B) \\\ & \Rightarrow y=2Sin(\omega t+{{60}^{\circ }}) \\\ \end{aligned}$
The above equation represents the equation of simple harmonic motion, i.e. $y=A\sin (\omega t+\phi )$ where A is the amplitude of displacement from the mean position, $\omega$ is the angular frequency of vibration and $\phi$ is the phase of the S.H.M and y is the displacement of the body at time ‘t’.

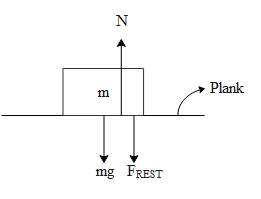
In the above figure we can see that the mass m is kept on the plank executing S.H.M. The body of mass m will just break off the plank when the restoring force acts downwards. Let us say the restoring force of the above system be (${{F}_{\operatorname{REST}}}$=ma)where a is the net acceleration of the body with mass m. hence the net force on the above body can be written as,
$mg-N=ma$
When the body loses contact with the plank the normal force N goes to zero. Hence the above equation becomes,
$\begin{aligned} & mg=ma \\\ & \Rightarrow g=a \\\ \end{aligned}$
For a body performing S.H.M the acceleration a can be written as,
$a={{\omega }^{2}}y$
Hence the value of the angular frequency from the equations of a we get,
$\begin{aligned} & g={{\omega }^{2}}y \\\ & \Rightarrow \omega =\sqrt{\dfrac{g}{y}}...(1) \\\ \end{aligned}$
In the question we are asked to determine the minimum value of angular frequency. But if we look at the above equation this is only possible when the value of y is maximum. Hence we will have to differentiate the equation of motion of the body of mass m to obtain the point of maxima of y.
$\begin{aligned} & y=\sin \omega t+\sqrt{3}\cos \omega t \\\ & \dfrac{dy}{dx}=\dfrac{d\sin \omega t}{dx}+\sqrt{3}\dfrac{d\cos \omega t}{dx}\text{, }dx=\omega t \\\ & \dfrac{dy}{dx}=\cos \omega t-\sqrt{3}\sin \omega t \\\ \end{aligned}$
Point of maxima or minima is given at, $\dfrac{dy}{dx}=0$ .Therefore,
$\begin{aligned} & cos\omega t-\sqrt{3}\sin \omega t=0 \\\ & \Rightarrow \tan \omega t=\dfrac{1}{\sqrt{3}} \\\ & \Rightarrow \omega t={{30}^{\circ }} \\\ & But\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=-(\sin \omega t-\sqrt{3}cos\omega t) \\\ \end{aligned}$
The double derivative of the above equation of motion is negative. Hence The above value obtained for y is the point of maxima. Therefore the maximum value for y is,
$\begin{aligned} & y=\sin {{30}^{\circ }}+\sqrt{3}\cos {{30}^{\circ }} \\\ & \Rightarrow y=\dfrac{1}{2}+\sqrt{3}\dfrac{\sqrt{3}}{2}=\dfrac{1+3}{2}=2 \\\ \end{aligned}$
Therefore from equation 1 the minimum value of y is,
$\begin{aligned} & \omega =\sqrt{\dfrac{g}{y}} \\\ & \Rightarrow \omega =\sqrt{\dfrac{g}{2}} \\\ \end{aligned}$
Further we asked to determine the instance of time with respect to t=0 for which the breaking off of the mass with the plank takes place. We have found that $\omega t={{30}^{\circ }}$ . This in terms of radians can be expressed as,
$\begin{aligned} & \omega t={{30}^{\circ }} \\\ & \Rightarrow \omega t=\dfrac{\pi }{6}\text{, }\omega \text{=}\sqrt{\dfrac{g}{2}} \\\ & \Rightarrow t\sqrt{\dfrac{g}{2}}=\dfrac{\pi }{6} \\\ & \Rightarrow t=\dfrac{\pi }{6}\sqrt{\dfrac{2}{g}} \\\ \end{aligned}$

So, the correct answer is “Option A”.

Note:
When the restoring force acts downwards, one can think of the body as having no normal reaction. From this we can say that as the body is subjected to no normal force it’s no longer in contact with respect to something. Hence we have taken normal force to be zero when the body breaks off with the plank.