Solveeit Logo
Login

Question

Question: Verify that median divides a triangle into two triangles of equal areas for \( \Delta ABC \) whose v...

Verify that median divides a triangle into two triangles of equal areas for ΔABC\Delta ABC whose vertices are A(4,−6)A\left( 4,-6 \right) , B(3,−2)B\left( 3,-2 \right) , C(5,2)C\left( 5,2 \right) .

Explanation

Solution

Hint : We first take the vertices of ΔABC\Delta ABC and try to find the median AD where D is the midpoint of BC. Then we take the midpoint theorem of (a+c2,b+d2)\left( \dfrac{a+c}{2},\dfrac{b+d}{2} \right) for finding D. after that we find the area of the divided triangles to find the equality.

Complete step by step solution:
We have ΔABC\Delta ABC whose vertices are
A(4,−6)A\left( 4,-6 \right) , B(3,−2)B\left( 3,-2 \right) , C(5,2)C\left( 5,2 \right) .
We know that for given coordinates of vertices of
(a,b);(c,d);(e,f)\left( a,b \right);\left( c,d \right);\left( e,f \right) , the area of the triangle made out of those vertices will be
12∣a(d−f)+c(f−b)+e(b−d)∣\dfrac{1}{2}\left| a\left( d-f \right)+c\left( f-b \right)+e\left( b-d \right) \right| square unit.
We assume that for ΔABC\Delta ABC , the median is AD where D is the midpoint of BC.
We know that for given coordinates of vertices of (a,b);(c,d)\left( a,b \right);\left( c,d \right) , the midpoint will be (a+c2,b+d2)\left( \dfrac{a+c}{2},\dfrac{b+d}{2} \right).
We find the coordinates of D. So, following the mid-point theorem for B(3,−2)B\left( 3,-2 \right) , C(5,2)C\left( 5,2 \right) , we get
D≡(3+52,−2+22)≡(4,0)D\equiv \left( \dfrac{3+5}{2},\dfrac{-2+2}{2} \right)\equiv \left( 4,0 \right).

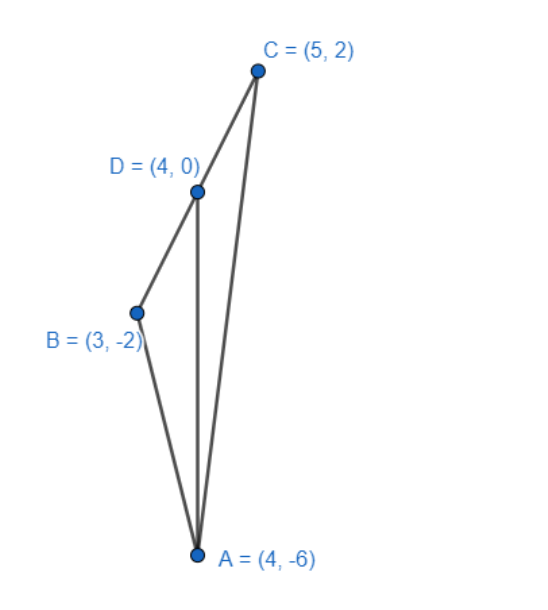
Now we find the areas for ΔABD\Delta ABD and ΔACD\Delta ACD .
For ΔABD\Delta ABD , the vertices are A(4,−6)A\left( 4,-6 \right) , B(3,−2)B\left( 3,-2 \right) , D(4,0)D\left( 4,0 \right) .
Therefore, the area is 12∣4(−2)+3(0+6)+4(−6+2)∣=62=3\dfrac{1}{2}\left| 4\left( -2 \right)+3\left( 0+6 \right)+4\left( -6+2 \right) \right|=\dfrac{6}{2}=3 square units.
For ΔACD\Delta ACD , the vertices are A(4,−6)A\left( 4,-6 \right) , C(5,2)C\left( 5,2 \right) , D(4,0)D\left( 4,0 \right) .
Therefore, the area is 12∣4(2)+5(0+6)+4(−6−2)∣=62=3\dfrac{1}{2}\left| 4\left( 2 \right)+5\left( 0+6 \right)+4\left( -6-2 \right) \right|=\dfrac{6}{2}=3 square units.
We can see that ar(ΔABD)=ar(ΔACD)=3ar\left( \Delta ABD \right)=ar\left( \Delta ACD \right)=3.
Thus, Verified that the median divides a triangle into two triangles of equal areas.

Note : Instead of taking AD, we could also have taken the medians like BE and CF. The final claim of getting triangles of equal areas remains the same for all medians.