Question

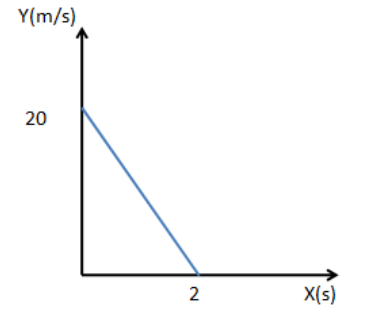
Velocity – time graph of a particle of mass $2kg$ moving in a straight line is as shown in the figure. Work done by all the forces on the particle is :

a. $400J$
b. $- 400J$
c. $- 200J$
d. $200J$

Answer 1

The velocity-time graph shows the value of velocity along the y-axis with respect to time along the x-axis. Find the acceleration from the given velocity and time.
The force is the product of the mass of the object and the acceleration.
The amount of the work-done is gained by the product of the force and the displacement.
Note that, we can find the displacement by calculating the area covered by the figure in the velocity-time graph.

Formula used:
Acceleration $a = \dfrac{{v{\text{(velocity)}}}}{{t{\text{(time)}}}}$
Now the applied force can be written as $F = m \times a$ , here $m$ is known as the mass of the object
The work-done $W = F \times s$
$s =$ the displacement = the area of the triangle that covers the velocity-time graph
$= \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
$= \dfrac{1}{2}vt$

Complete step by step answer:
The above graph is a velocity-time graph where the velocity is along the y-axis and the time is along the x-axis.
Given that, the velocity, $v = 20m/s$ at time $t = 2\sec$
So the Acceleration
$a = \dfrac{{v{\text{(velocity)}}}}{{t{\text{(time)}}}}$
$a = \dfrac{{20}}{2} = 10m/{s^2}$
The mass of the object $m = 2kg$
The applied force $F = m \times a = 2 \times 10 = 20N$

We know the work done is defined by the product of the applied force on an object and the displacement of that object due to this force.
Hence, The work-done $W = F \times s$

Now the displacement is calculated by measuring the area of the triangle shown in the graph.
$s = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
$\Rightarrow s = \dfrac{1}{2} \times 2 \times {\text{20}}$
$s = 20m$
So, The work-done $W = F \times s = 20 \times 20$
$\Rightarrow W = 400J$
So the work-done by the forces acting on the object is $W = 400J$

Hence, the correct answer is option (A).

Note: The slope of the graph represents the acceleration of the particle, it can be written as $a = \dfrac{{dv}}{{dt}}$ which is the ratio of velocity change and time change getting from the graph.
The area of the triangle defines the displacement of the particle in a velocity-time graph.
The unit of displacement is meter. So if we find this from the area of the triangle it will be $s = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$ which is $= \dfrac{1}{2}vt$. And from this we get
$\dfrac{1}{2} \times \dfrac{{{\text{meter}}}}{{\sec }} \times {\text{sec = }}\dfrac{{{\text{meter}}}}{2}$.