Question
Question: Vectors \(\overrightarrow{A}\) and \(\overrightarrow{B}\) are shown. What is the magnitude of a vect...
Vectors A and B are shown. What is the magnitude of a vector C if C=A−B?
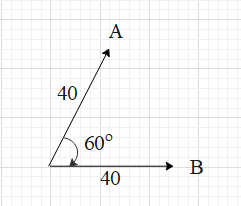
A. 403
B. 402
C. 40
D. 20
Solution
Draw the vector (−B) and find the angle between the vectors A and (−B). The magnitude of vector (−B) is equal to the magnitude of vector B. However, both the vectors are opposite directions. Then use the formula for the magnitude of the resultant of two vectors.
Formula used: R=A2+B2+2ABcosθ
Complete step by step answer:
The vectors A and B are given. We are asked to find the magnitude of the vector C=A−B. This vector addition can also be written as C=A+(−B).
Let us first draw the vector (−B). Vector (−B) is a vector whose magnitude is equal to the magnitude of vector B but its direction is opposite to the direction of B (as shown).
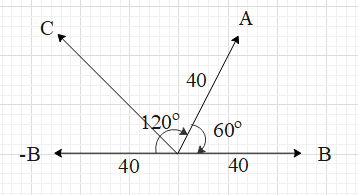
From the figure we get to know that the angle between the vectors A and (−B) is 120∘.
Let us know use the formula for the magnitude of the resultant of the two vectors, i.e. R=A2+B2+2ABcosθ ….. (i), where are R is the magnitude of the resultant, A and B are the magnitudes of the two vectors and θ is the angle between the two vectors.
In this case, R = C, A = 40.
The magnitude of (−B) is equal to the magnitude of B. Therefore, B = 40.
And θ=120∘.
Substitute the values in (i).
⇒C=402+402+2(40)(40)cos120∘.
The value of cos120∘=−21.
⇒C=402+402+2(40)(40)(−21)=402+402−402=402=40.
This means that the magnitude of C is 40.
So, the correct answer is “Option C”.
Note: Alternative solution:
The magnitude of resultant of C=A−B, is given as C=A2+B2−2ABcosθ ….. (1), where θ is the angle between the two vectors A and B.
Therefore, A = B = 40 and θ=60∘.
Substitute the values in (1).
⇒C=402+402−2(40)(40)cos60∘=402+402−2(40)(40)(21)=402+402−402=402=40.
