Question

Vector $\overrightarrow Q$ ​ has a magnitude of $8$ is added to the vector $\overrightarrow P$ which lies along the X-axis. The resultant of these two vectors is a third vector $\overrightarrow R$ which lies along the Y-axis and has a magnitude twice that of $\overrightarrow P$ . The magnitude of $\overrightarrow P$ is:
(A) $\dfrac{6}{{\sqrt 5 }}$
(B) $\dfrac{8}{{\sqrt 5 }}$
(C) $\dfrac{{12}}{{\sqrt 5 }}$
(D) $\dfrac{{16}}{{\sqrt 5 }}$

Answer 1

Vector $\overrightarrow P$ is along the x-axis and vector $\overrightarrow R$ is along the y-axis. So they make an angle of ${90^ \circ }$ with each other. Use this to find the relation between vector $\overrightarrow P$ and angle between vector $\overrightarrow Q$ and vector $\overrightarrow P$ . Then use the formula to find the resultant of two vectors, we will get our required magnitude of the vector $\overrightarrow P$

Complete Step By Step Answer:

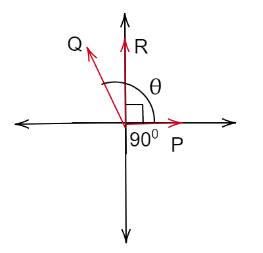
We have been given that the magnitude of the vector $\overrightarrow Q = 8$
We can see from the above graph vector $\overrightarrow R$ is perpendicular to the vector $\overrightarrow P$
For finding the relation between vector $\overrightarrow Q$ and vector $\overrightarrow P$
$\tan {90^ \circ } = \dfrac{{Q\sin \theta }}{{P + Q\cos \theta }}$
Putting the value of the vector $\overrightarrow Q$
$\Rightarrow \tan {90^ \circ } = \dfrac{{8\sin \theta }}{{P + 8\cos \theta }}$
$\because \tan {90^ \circ } = \infty$
$\Rightarrow P + 8\cos \theta = 0$
$\Rightarrow \cos \theta = \dfrac{{ - P}}{8}$
Now finding the resultant to get the relation between all three vectors,
$\left| {\overrightarrow R } \right| = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta }$
Above is the equation for the product of two vectors, where $\overrightarrow P$ and $\overrightarrow Q$ are the magnitudes of the vectors and $\theta$ is the angle between them.
We have been given vector $\overrightarrow R$ is twice of vector $\overrightarrow P$
Putting the values of vector $\overrightarrow R$ and $\cos \theta$ in the above equation
$\Rightarrow \left( {2P} \right) = \sqrt {{P^2} + {8^2} + 2P(8)\left( {\dfrac{{ - P}}{8}} \right)}$
$\Rightarrow {(2P)^2} = {P^2} + {8^2} - 2{P^2}$
$\Rightarrow 5{P^2} = 64$
$\Rightarrow P = \sqrt {\dfrac{{64}}{5}}$
$\Rightarrow P = \dfrac{8}{{\sqrt 5 }}$
Therefore the magnitude of the vector $\overrightarrow P$ is found to be $\dfrac{8}{{\sqrt 5 }}$
Hence, option B) $\dfrac{8}{{\sqrt 5 }}$ is the correct option.

Note:
The length of the vector is known as the magnitude of the vector. The resultant of any two vectors is equal to the vector sum of those two vectors. For $\tan {90^ \circ } = \infty$ the denominator has to be zero that is why we got $P + 8\cos \theta = 0$ .