Question

Vector $M$ of magnitude $5$ cm, is at ${36.9^ \circ }$ counter clockwise from the +X axis. It is added to vector $N$ , and the resultant is a vector of magnitude $5$ cm at ${53.1^ \circ }$ clockwise from +X axis. Find the magnitude of $N$
A. $5\sqrt 2$
B. $9\sqrt 2$
C. $3\sqrt 2$
D. $7\sqrt 2$

Answer 1

To find the magnitude of $N$ , we have to draw the vectors on the graph and find the angle between the vectors to find the magnitude of the vectors by using Pythagoras’ theorem. We use the concept of positive and negative angles from the origin.

Complete step by step answer:
We are given that, vector $M$ of magnitude $5$ cm is ${36.9^ \circ }$ counter clockwise from +X axis is added to vector $N$, the resultant vector is of magnitude $5$ cm is ${53.1^ \circ }$ clockwise from +X axis. Representing these vectors, we have

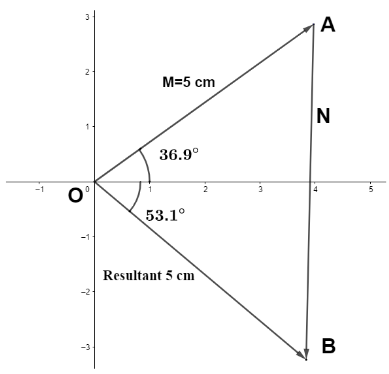
Vector $M$, $N$ and the resultant of $M\& N$ makes a right angled triangle.So, using Pythagoras’ theorem in $\Delta AOB$, we have
Magnitude of vector $N$= $\therefore \left| N \right| = \sqrt {O{A^2} + O{B^2}}$
$\left| N \right| = \sqrt {{5^2} + {5^2}}$
$\therefore \left| N \right| = 5\sqrt 2$ cm
The magnitude of $N$ is $5\sqrt 2$ cm.

Hence, option A is correct.

Note: We should use the positive and negative angles notation for counterclockwise and clockwise angles, respectively. We can also use the triangle law of addition of the vectors which states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.