Solveeit Logo
Login

Question

Question: Value of $\frac{29\int_{0}^{1}(1-x^4)^7dx}{4\int_{0}^{1}(1-x^4)^6dx}$ is equal to...

Value of 29∫01(1−x4)7dx4∫01(1−x4)6dx\frac{29\int_{0}^{1}(1-x^4)^7dx}{4\int_{0}^{1}(1-x^4)^6dx} is equal to

Answer

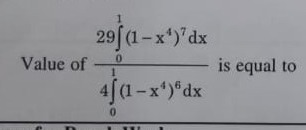
7

Explanation

Solution

Let the given expression be EE. E=29∫01(1−x4)7dx4∫01(1−x4)6dxE = \frac{29\int_{0}^{1}(1-x^4)^7dx}{4\int_{0}^{1}(1-x^4)^6dx}

Let In=∫01(1−x4)ndxI_n = \int_{0}^{1}(1-x^4)^n dx. The expression can be written as E=29I74I6E = \frac{29 I_7}{4 I_6}.

We use integration by parts to find a reduction formula for InI_n. In=∫01(1−x4)ndxI_n = \int_{0}^{1}(1-x^4)^n dx. Let u=(1−x4)nu = (1-x^4)^n and dv=dxdv = dx. Then du=n(1−x4)n−1(−4x3)dx=−4nx3(1−x4)n−1dxdu = n(1-x^4)^{n-1}(-4x^3)dx = -4nx^3(1-x^4)^{n-1}dx and v=xv = x. Applying the integration by parts formula ∫udv=uv−∫vdu\int u dv = uv - \int v du: In=[x(1−x4)n]01−∫01x(−4nx3(1−x4)n−1)dxI_n = [x(1-x^4)^n]_0^1 - \int_{0}^{1}x(-4nx^3(1-x^4)^{n-1})dx Evaluate the term [x(1−x4)n]01[x(1-x^4)^n]_0^1: [x(1−x4)n]01=1(1−14)n−0(1−04)n=1(0)n−0(1)n=0−0=0[x(1-x^4)^n]_0^1 = 1(1-1^4)^n - 0(1-0^4)^n = 1(0)^n - 0(1)^n = 0 - 0 = 0 (assuming n≥1n \ge 1). So, In=0−∫01(−4nx4(1−x4)n−1)dxI_n = 0 - \int_{0}^{1}(-4nx^4(1-x^4)^{n-1})dx In=4n∫01x4(1−x4)n−1dxI_n = 4n\int_{0}^{1}x^4(1-x^4)^{n-1}dx

Now, we manipulate the integrand x4(1−x4)n−1x^4(1-x^4)^{n-1} to relate it to InI_n and In−1I_{n-1}. x4(1−x4)n−1=(x4−1+1)(1−x4)n−1=(−(1−x4)+1)(1−x4)n−1x^4(1-x^4)^{n-1} = (x^4 - 1 + 1)(1-x^4)^{n-1} = (-(1-x^4) + 1)(1-x^4)^{n-1} x4(1−x4)n−1=−(1−x4)(1−x4)n−1+1⋅(1−x4)n−1x^4(1-x^4)^{n-1} = -(1-x^4)(1-x^4)^{n-1} + 1 \cdot (1-x^4)^{n-1} x4(1−x4)n−1=−(1−x4)n+(1−x4)n−1x^4(1-x^4)^{n-1} = -(1-x^4)^n + (1-x^4)^{n-1}

Substitute this back into the expression for InI_n: In=4n∫01[−(1−x4)n+(1−x4)n−1]dxI_n = 4n\int_{0}^{1}[-(1-x^4)^n + (1-x^4)^{n-1}]dx In=4n[−∫01(1−x4)ndx+∫01(1−x4)n−1dx]I_n = 4n\left[-\int_{0}^{1}(1-x^4)^n dx + \int_{0}^{1}(1-x^4)^{n-1} dx\right] In=4n(−In+In−1)I_n = 4n(-I_n + I_{n-1}) In=−4nIn+4nIn−1I_n = -4nI_n + 4nI_{n-1} In+4nIn=4nIn−1I_n + 4nI_n = 4nI_{n-1} (1+4n)In=4nIn−1(1+4n)I_n = 4nI_{n-1} In=4n4n+1In−1I_n = \frac{4n}{4n+1}I_{n-1}

This is the reduction formula for InI_n. We need to find the value of 29I74I6\frac{29 I_7}{4 I_6}. Using the reduction formula for n=7n=7: I7=4×74×7+1I7−1I_7 = \frac{4 \times 7}{4 \times 7 + 1}I_{7-1} I7=2828+1I6I_7 = \frac{28}{28 + 1}I_6 I7=2829I6I_7 = \frac{28}{29}I_6

Now substitute this expression for I7I_7 into the given expression EE: E=29I74I6E = \frac{29 I_7}{4 I_6} E=29(2829I6)4I6E = \frac{29 \left(\frac{28}{29}I_6\right)}{4 I_6} E=28I64I6E = \frac{28 I_6}{4 I_6}

Since I6=∫01(1−x4)6dxI_6 = \int_{0}^{1}(1-x^4)^6dx, and for x∈(0,1)x \in (0, 1), x4∈(0,1)x^4 \in (0, 1), so 1−x4∈(0,1)1-x^4 \in (0, 1). Thus (1−x4)6>0(1-x^4)^6 > 0 for x∈(0,1)x \in (0, 1). The integral of a positive function over an interval of non-zero length is positive, so I6>0I_6 > 0. We can cancel I6I_6 from the numerator and the denominator. E=284E = \frac{28}{4} E=7E = 7