Question

value of (csc A - sec 2A).

*Q.7 Let $A_1, A_2, A_3 \dots A_n$ are the vertices of a regular n sided polygon inscribed in a circle of radius R. If $(A_1 A_2)^2 + (A_1 A_3)^2 + \dots + (A_1 A_n)^2 = 14R^2$, find the number of sides in the polygon.

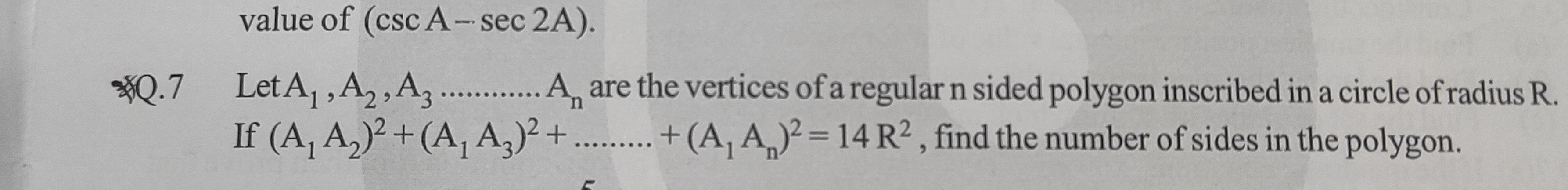
Answer 1

csc A – sec 2A: It cannot be numerically evaluated without extra conditions on A; the simplified form is (1/sin A) – (1/cos 2A). Number of sides in the polygon (Q.7): 7

Answer 2

The value of csc A - sec 2A cannot be determined without additional information about A. For the polygon problem, the sum of the squares of the distances from one vertex to all other vertices of a regular n-sided polygon inscribed in a circle of radius R is 2nR^2. Setting this equal to 14R^2, we find n = 7.