Question

Value of

$\begin{vmatrix} a.a & a.b \\ a.b & b.b \end{vmatrix}$ is equal to

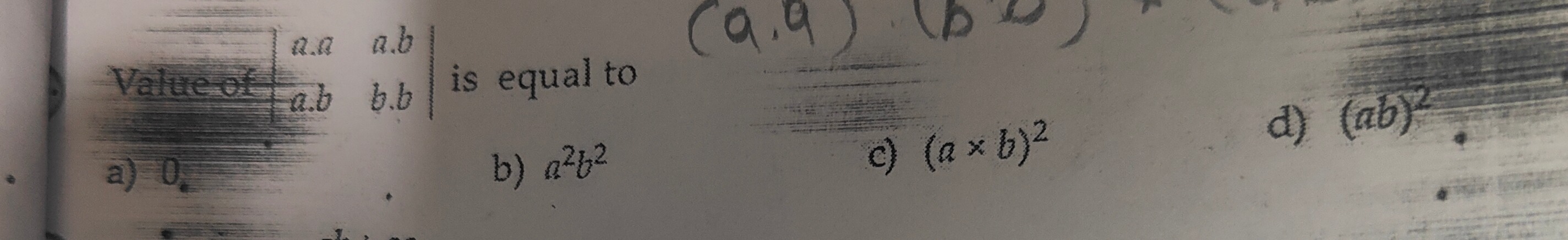
• A. 0
• B. $a^2b^2$
• C. $(a \times b)^2$
• D. $(ab)^2$

Answer 1

Answer: (C)

$(a \times b)^2$

Answer 2

The determinant is given by

$$\begin{vmatrix} \mathbf{a}\cdot\mathbf{a} & \mathbf{a}\cdot\mathbf{b} \\ \mathbf{a}\cdot\mathbf{b} & \mathbf{b}\cdot\mathbf{b} \end{vmatrix} = (\mathbf{a}\cdot\mathbf{a})(\mathbf{b}\cdot\mathbf{b}) - (\mathbf{a}\cdot\mathbf{b})^2.$$

Recognize that

$$(\mathbf{a} \times \mathbf{b})^2 = a^2b^2 - (\mathbf{a}\cdot\mathbf{b})^2,$$

where $a^2 = \mathbf{a}\cdot\mathbf{a}$ and $b^2 = \mathbf{b}\cdot\mathbf{b}$. Thus, the determinant equals $(\mathbf{a} \times \mathbf{b})^2$.