Question
Question: $\int_{0}^{\infty} \frac{\ln x}{x^2 + kx + k^2} dx$, where k > 0....
∫0∞x2+kx+k2lnxdx, where k > 0.
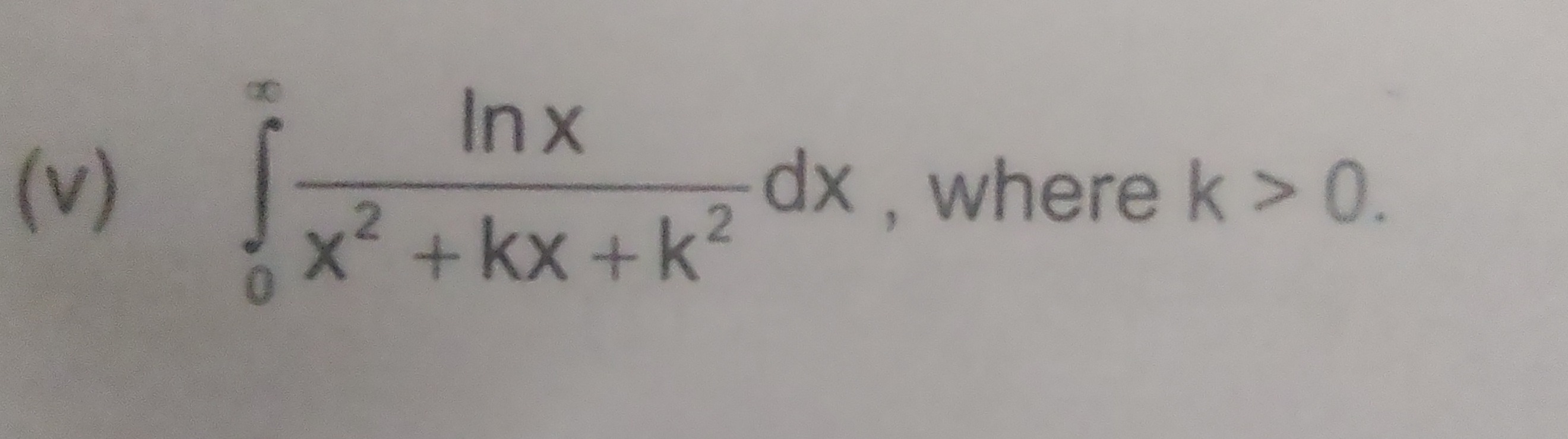
33k2πlnk
Solution
The problem asks to evaluate the definite integral I=∫0∞x2+kx+k2lnxdx, where k>0.
Explanation of the Solution:
-
Identify the general form and apply a known property: The integral is of the form ∫0∞x2+ax+blnxdx. A common property for such integrals states that if b>0, then I=2lnb∫0∞x2+ax+b1dx. In our given integral, a=k and b=k2. Since k>0, b=k2>0. Applying the property: I=2ln(k2)∫0∞x2+kx+k21dx I=22lnk∫0∞x2+kx+k21dx I=lnk∫0∞x2+kx+k21dx
-
Evaluate the remaining integral: We need to evaluate J=∫0∞x2+kx+k21dx. Complete the square in the denominator: x2+kx+k2=x2+kx+(2k)2−(2k)2+k2 =(x+2k)2+k2−4k2 =(x+2k)2+43k2 =(x+2k)2+(23k)2
Now, substitute u=x+2k. Then du=dx. The limits of integration change: When x=0, u=0+2k=2k. When x=∞, u=∞+2k=∞. So, the integral becomes: J=∫k/2∞u2+(23k)21du
This is a standard integral of the form ∫y2+A21dy=A1arctan(Ay). Here, A=23k. J=[23k1arctan(23ku)]k/2∞ J=3k2[arctan(3k2u)]k/2∞ J=3k2(limu→∞arctan(3k2u)−arctan(3k2(k/2))) J=3k2(arctan(∞)−arctan(3kk)) J=3k2(2π−arctan(31)) J=3k2(2π−6π) J=3k2(63π−π) J=3k2(62π) J=3k2(3π) J=33k2π
-
Combine the results: Substitute the value of J back into the expression for I: I=lnk⋅J I=lnk⋅33k2π I=33k2πlnk
