Question

$(1 + \sin^2x)^2 (1 + \cos^2x)^3$

Answer 1

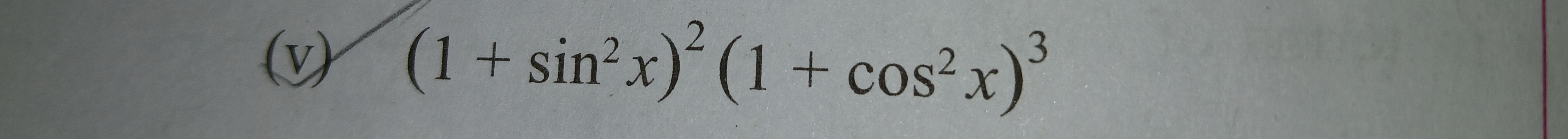
The expression $(1+\sin^2x)^2 (1+\cos^2x)^3$ has a minimum value of $4$ and a maximum value of $\frac{26244}{3125}$.

Answer 2

We wish to find the range (maximum and minimum values) of

$$E(x)=(1+\sin^2x)^2(1+\cos^2x)^3.$$

Step 1. Express in a single variable

Since

$$\sin^2x+\cos^2x=1,$$

let

$$t=\sin^2x\quad \text{so that}\quad \cos^2x=1-t.$$

Then

$$E(x)=f(t)=(1+t)^2\Bigl(1+(1-t)\Bigr)^3=(1+t)^2(2-t)^3,\quad t\in [0,1].$$

Step 2. Find the endpoints

At $t=0$:

$$f(0)=(1+0)^2(2-0)^3=1^2\cdot2^3=8.$$

At $t=1$:

$$f(1)=(1+1)^2(2-1)^3=2^2\cdot 1^3=4.$$

Step 3. Find the critical point

Differentiate $f(t)$ using logarithmic differentiation:

$$\ln f(t)=2\ln(1+t)+3\ln(2-t).$$

Differentiate with respect to $t$:

$$\frac{f'(t)}{f(t)}=\frac{2}{1+t} - \frac{3}{2-t}.$$

Set $\frac{f'(t)}{f(t)}=0$:

$$\frac{2}{1+t} = \frac{3}{2-t} \quad \Longrightarrow \quad 2(2-t)=3(1+t).$$

Simplify:

$$4-2t=3+3t\quad\Longrightarrow\quad 4-3=3t+2t,\quad 1=5t,\quad t=\frac{1}{5}.$$

Step 4. Evaluate at the critical point

When $t=\frac{1}{5}$:

$$f\Bigl(\frac{1}{5}\Bigr)=\left(1+\frac{1}{5}\right)^2\left(2-\frac{1}{5}\right)^3.$$

Compute:

$$1+\frac{1}{5}=\frac{6}{5},\quad 2-\frac{1}{5}=\frac{9}{5}.$$

Thus,

$$f\Bigl(\frac{1}{5}\Bigr)=\Bigl(\frac{6}{5}\Bigr)^2\Bigl(\frac{9}{5}\Bigr)^3 = \frac{36}{25}\cdot \frac{729}{125} =\frac{36\times729}{3125}=\frac{26244}{3125}.$$

Step 5. Determine the range

We found:

• At $t=1$, $f(1)=4$ (minimum).
• At $t=0$, $f(0)=8$.
• At $t=\frac{1}{5}$, $f\Bigl(\frac{1}{5}\Bigr)=\frac{26244}{3125}\approx 8.3981$ (maximum).

Thus, the expression attains its minimum value $4$ and maximum value $\frac{26244}{3125}$.

---

Core Explanation:
Substitute $\sin^2x=t$ so that $\cos^2x=1-t$, getting $f(t)=(1+t)^2(2-t)^3$. Differentiate $f(t)$ (or use the logarithmic derivative) to find the critical point $t=\frac{1}{5}$. Evaluate $f(t)$ at $t=0$, $t=1$, and $t=\frac{1}{5}$ to obtain the range $[4,\frac{26244}{3125}]$.