Question

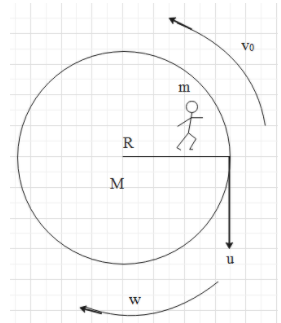
UUHU Board of mass Maddie Bie placed on to rotate about a fixed axis which passes through its centre Ur mass M and radius R is placed on a fixed smooth horizontal plane and is free marked A on the circumference of the board. At first, it passes through its centre. A man of mass m is standing on the point Werence of the board. At first, the board & the man are at rest. The man starts moving along the rim of the board at constant speed $v_0$ relative to the bo rotation when the man passes his starting point on the disc The board at a constant speed v. relative to the board. Find the angle of board A point object of money.

Answer 1

The angle of the board is the product of angular frequency and the period of motion. Thus, using the formula of rotational velocity, find the values of angular frequency and the period of motion and then multiply them, the required result will be obtained.

Formula used:
$s=\dfrac{d}{t}$

Complete answer:
From given, we have,
The mass of the board = M
The radius of the board = R
The mass of a man = m
The constant speed of the board = ${{v}_{0}}$

As in the case of a round trip, an object travels a length equal to that of the circumference of the circle. Therefore, the tangential velocity, also called the rotational velocity can be found as follows.
The diagram representing the motion of the board.

The object’s speed is given by,
$s=\dfrac{d}{t}$
The time to go around once is T
The circumference of the circle is given by,
$C=2\pi r$
Thus, the rotational velocity is given as follows:
$V=\dfrac{2\pi r}{T}$
Therefore, the expression in terms of the period of motion is given as follows.
$T=\dfrac{2\pi r}{V}$
Now substitute the given values in the above equation.
So, we get,
$t=\dfrac{2\pi R}{{{v}_{0}}}$ …… (1)
Now find out the expression for the angular frequency.
The expression for angular frequency is calculated as follows.

& w=2\pi f \\\ & \Rightarrow f=\dfrac{1}{T} \\\ & \Rightarrow w=\dfrac{2\pi }{T} \\\ \end{aligned}$$ Now substitute the value of the period of motion obtained in the above equation to further reduce the equation. $$\begin{aligned} & w=\dfrac{2\pi }{{}^{2\pi r}/{}_{V}} \\\ & \Rightarrow w=\dfrac{V}{r} \\\ \end{aligned}$$ Now substitute the given values in the above equation. So, we get, $$w=\dfrac{u}{R}$$ …… (2) From given, we get the value of the initial velocity as follows. $$u={{v}_{0}}\left( \dfrac{m}{M} \right)$$ …… (3) Now combine all the equations (1), (2) and (3) to obtain the value of the angle by which the board turned. Therefore, the angle turned by the board is the product of the angular frequency and the period of motion. So, in the form of equation, we obtain the angle as, $$\begin{aligned} & \theta =wt \\\ & \Rightarrow \theta =\dfrac{u}{R}\times \dfrac{2\pi R}{{{v}_{0}}} \\\ & \Rightarrow \theta =u\times \dfrac{2\pi }{{{v}_{0}}} \\\ \end{aligned}$$ At this stage, substitute the value of the initial velocity. So, we get, $$\begin{aligned} & \theta ={{v}_{0}}\left( \dfrac{m}{M} \right)\times \dfrac{2\pi }{{{v}_{0}}} \\\ & \Rightarrow \theta =\left( \dfrac{m}{M} \right)\times 2\pi \\\ \end{aligned}$$ Therefore, the angle turn of the board is given as follows. $$\theta =2\pi \left( \dfrac{m}{M} \right)\,rad$$ Therefore, the angle turned by the board is given as $$2\pi \left( \dfrac{m}{M} \right)\,rad$$. **Note:** The things to be on your finger-tips for further information on solving these types of problems are: The units of the parameters should be taken into consideration while solving the problem. The unit of the angle should also be taken care of.