Question

Using vectors, prove that angle in a semicircle is a right angle.

Answer 1

Hint: Before attempting this question one should have prior knowledge of vector method and also remember to use the triangle law of vector i.e. $\overrightarrow {BA} = \overrightarrow {BO} + \overrightarrow {OA}$, use this information to approach towards the solution to the question.

Complete step-by-step solution -
Let take a semi-circle with center O
Now constructing vectors$\overrightarrow {BA} ,\overrightarrow {BO} ,\overrightarrow {OA} ,\overrightarrow {BC}$ and $\overrightarrow {OC}$ in the semicircle here magnitude of $\overrightarrow {OA}$ and $\overrightarrow {OC}$ is equal to the radius

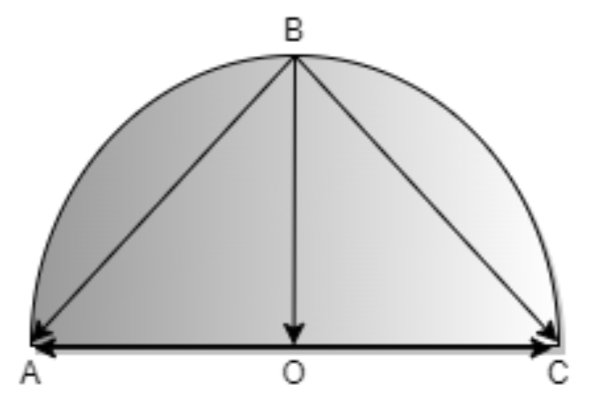
By the diagram given above we can say that since magnitude of $\overrightarrow {OA}$ and $\overrightarrow {OC}$ are equal and opposite therefore $\overrightarrow {OA} = - \overrightarrow {OC}$
Now using the triangle law of vector in triangle BOA we get
So, $\overrightarrow {BA} = \overrightarrow {BO} + \overrightarrow {OA}$ taking this as equation 1
Now using the triangle law of vector in triangle BOC we get
So, $\overrightarrow {BC} = \overrightarrow {BO} + \overrightarrow {OC}$ taking this as equation 2
Since we know that $\overrightarrow {OA} = - \overrightarrow {OC}$ substituting this in equation 1 and multiplying equation 1 and equation 2 we get
$\overrightarrow {BA} .\overrightarrow {BC} = \left( {\overrightarrow {BO} - \overrightarrow {OC} } \right)\left( {\overrightarrow {BO} + \overrightarrow {OC} } \right)$
$\Rightarrow$ $\overrightarrow {BA} .\overrightarrow {BC} = \overrightarrow {{{\left( {BO} \right)}^2}} - \overrightarrow {{{\left( {OC} \right)}^2}}$
Since we know that $\overrightarrow {OC}$ and $\overrightarrow {BO}$ have magnitude equal to radius of the semi-circle i.e. $\overrightarrow {OC}$ = $\overrightarrow {BO}$ = $\overrightarrow r$
Therefore $\overrightarrow {BA} .\overrightarrow {BC} = \overrightarrow {{r^2}} - \overrightarrow {{r^2}}$
$\Rightarrow$ $\overrightarrow {BA} .\overrightarrow {BC}$ = 0
As we know that whenever the dot product of 2 vectors is 0 it means that the 2 vectors are perpendicular to each other
Therefore it means $\overrightarrow {BA}$ and $\overrightarrow {BC}$ are perpendicular to each other
Thus it means $\angle ABC = {90^ \circ }$
Hence proved that the angle of semicircle is a right angle.

Note: The term” triangle law of vector” we used in the above solution can be explained as when the two vectors that represent the two sides of triangle having some order of magnitude and direction then the third side of the triangle represents the resultant vector of the both vectors and also defines the direction and magnitude of the resultant vector. In this law of triangle for vector the two vectors which represents the sides of triangle should be arranged in such a way that the head of first vector should touch the tail of the second vector and the resultant vector will touch the head to head with second vector and tail to tail with first vector.