Question

Using Truth tables, examine whether the statement pattern ${\rm{(p}} \wedge {\rm{q)}} \vee {\rm{(p}} \wedge {\rm{r)}}$ is a tautology, contradiction or contingency.

Answer 1

Here in this question we have to use the concept of the truth table to find the values of the given equation. Firstly we have to write the truth table for the variables and find the values of the ${\rm{(p}} \wedge {\rm{q)}}$ and ${\rm{(p}} \wedge {\rm{r)}}$. Then we have to find the final values of the equation given in the question i.e. ${\rm{(p}} \wedge {\rm{q)}} \vee {\rm{(p}} \wedge {\rm{r)}}$. Then by the values which are obtained for the function, we have to identify its form i.e. whether it is a tautology, contradiction or contingency.

Complete step-by-step answer:
Given equation or pattern in the question is ${\rm{(p}} \wedge {\rm{q)}} \vee {\rm{(p}} \wedge {\rm{r)}}$ and we know that $\wedge$ stands for the AND gate and $\vee$ stands for the OR gate.
Firstly we have to write the truth table for the variables ${\rm{p,q,r}}$.

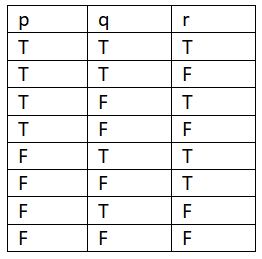
Now we have to find the values of the${\rm{(p}} \wedge {\rm{q)}}$ and ${\rm{(p}} \wedge {\rm{r)}}$. Therefore we get

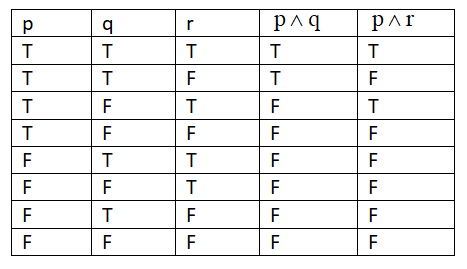
Now we have to find the value of the given equation or pattern, we get

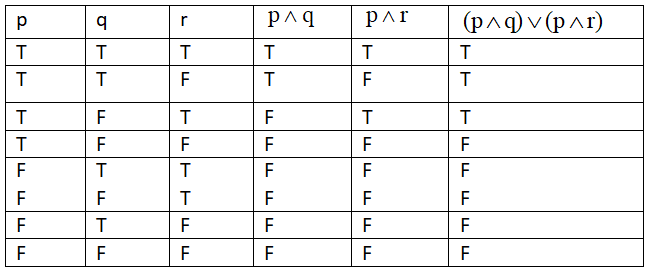
Now as we have got the values of the given equation. Now we have to identify what type of pattern it is.
So, from the table, we can clearly see that the pattern is of the contingency type.
Hence, the statement pattern${\rm{(p}} \wedge {\rm{q)}} \vee {\rm{(p}} \wedge {\rm{r)}}$ is contingency.
Note: We should know the meaning of tautology, contradiction or contingency. A statement pattern is said to be Tautology when the given statement pattern is always true. A statement pattern is said to be a Contradiction when the given statement pattern is always false. A statement pattern is said to be Contingency when the given statement pattern is neither always true nor always false. The truth table is the table in which the value of the variable can only be true or false.
AND gate is the logic gate that gives true value if and only if the values of all operands are true otherwise AND gate gives false.
OR gate is the logic gate that gives true value if at least value of one operand is true otherwise OR gate gives false.