Question

Using the method of integration, find the smaller area enclosed by the circle ${x^2} + {y^2} = 4$ and the line $x + y = 2$.

Answer 1

We can plot the given curves in the XY plane. Then we can find the limits of integration by finding the point of intersections of the curves. Then we can find the area under the circle by integrating with respect to y. Then we can find the area under the line by integrating the equation of the line with respect to x. Then we can find the required area by subtracting the area under the line from the area under the circle in the interval.

Complete step-by-step answer:
We can plot the given circle and line on the XY plane.

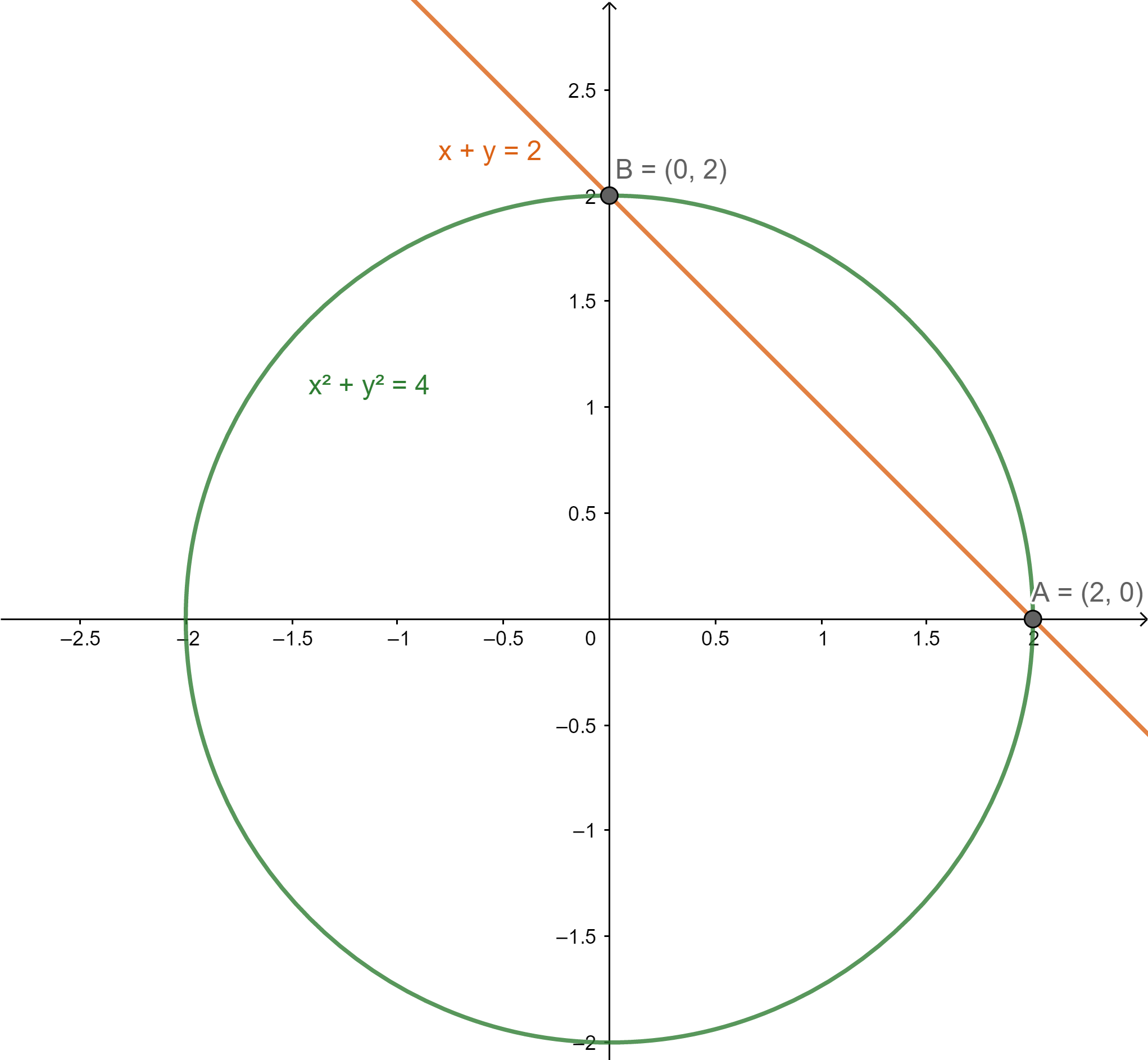
We need to find the area using integration. We can find the limits of integration by solving the equation.
We have the equations
${x^2} + {y^2} = 4$… (1)
And, $x + y = 2$
On rearranging, we get,
$\Rightarrow y = 2 - x$.. (2)
On substituting value of y from (2) in (1), we get,
$\Rightarrow {x^2} + {\left( {2 - x} \right)^2} = 4$
On expanding the square using the identity ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$, we get,
$\Rightarrow {x^2} + {2^2} - 2 \times 2 \times x + {x^2} = 4$
On simplification, we get,
$\Rightarrow {x^2} + 4 - 4x + {x^2} = 4$
On adding the like terms we get,
$\Rightarrow 2{x^2} - 4x = 0$
On taking 2x common we get,
$\Rightarrow 2x\left( {x - 2} \right) = 0$
Hence we have,
$\Rightarrow x = 0$or $x - 2 = 0$
$\Rightarrow x = 0,2$
So, the limit of integration is x=0 to x=2.
We need to find the smallest area enclosed by the circle and the line.
For that, we can subtract the area under the line from the area under the circle in the interval.
Now we can calculate the area under the circle.
We know that the area between x axis and the curve is given by, $A = \int\limits_a^b {ydx}$
The equation of the circle is ${x^2} + {y^2} = 4$. We can write it in terms of y.
$\Rightarrow {y^2} = 4 - {x^2}$
Taking square root we get,
$\Rightarrow y = \sqrt {4 - {x^2}}$
Then the area under circle is given by the equation,
${A_1} = \int\limits_0^2 {ydx}$
On substituting the value of y we get,
$\Rightarrow {A_1} = \int\limits_0^2 {\sqrt {4 - {x^2}} dx}$
We know that $\int {\sqrt {{a^2} - {x^2}} } = \dfrac{{{a^2}{{\sin }^{ - 1}}\left( {\dfrac{x}{a}} \right) + x\sqrt {{a^2} - {x^2}} }}{2} + C$.
$\Rightarrow {A_1} = \left[ {\dfrac{{{2^2}{{\sin }^{ - 1}}\left( {\dfrac{x}{2}} \right) + x\sqrt {{2^2} - {x^2}} }}{2}} \right]_0^2$
On applying the limits, we get,
$\Rightarrow {A_1} = \left[ {\dfrac{{4{{\sin }^{ - 1}}\left( {\dfrac{2}{2}} \right) + x\sqrt {{2^2} - {2^2}} }}{2}} \right] - \left[ {\dfrac{{4{{\sin }^{ - 1}}\left( {\dfrac{0}{2}} \right) + 0\sqrt {{2^2} - {0^2}} }}{2}} \right]$
On simplification, we get,
$\Rightarrow {A_1} = \left[ {\dfrac{{4{{\sin }^{ - 1}}\left( 1 \right) + 0}}{2}} \right] - \left[ {\dfrac{{4{{\sin }^{ - 1}}\left( 0 \right) + 0}}{2}} \right]$
We know that ${\sin ^{ - 1}}\left( 1 \right) = \dfrac{\pi }{2}$ and ${\sin ^{ - 1}}\left( 0 \right) = 0$
$\Rightarrow {A_1} = \left[ {2 \times \dfrac{\pi }{2}} \right] - \left[ 0 \right]$
On simplification we get,
$\Rightarrow {A_1} = \pi$
Now we can find the area under the line $y = 2 - x$. It is given by,
${A_2} = \int\limits_0^2 {ydx}$
Substituting value of y we get,
$\Rightarrow {A_2} = \int\limits_0^2 {\left( {2 - x} \right)dx}$
Using $\int {(a + b)dx = \int {a.dx + \int {b.dx} } }$ , we get,
$\Rightarrow {A_2} = \int\limits_0^2 {2dx} - \int\limits_0^2 {xdx}$
We know that $\int {dx} = x$and $\int {xdx} = \dfrac{{{x^2}}}{2}$,
$\Rightarrow {A_2} = 2\left[ x \right]_0^2 - \left[ {\dfrac{{{x^2}}}{2}} \right]_0^2$
On applying the limits, we get,
$\Rightarrow {A_2} = 2\left[ {2 - 0} \right] - \left[ {\dfrac{{{2^2} - 0}}{2}} \right]$
On simplification we get,
$\Rightarrow {A_2} = 4 - 2$
$\Rightarrow {A_2} = 2$
Therefore, the required area is given by,
$A = {A_1} - {A_2}$
On substituting the values, we get,
$\Rightarrow A = \pi - 2$
Therefore, the required area is $\pi - 2$ square units.

Note: Alternate method to solve this problem without integration is given by,
From the figure, the required area can be found by subtracting the area of the triangle formed by the line and axes from the area of the quarter of the circle.
From the equation of the circle, ${x^2} + {y^2} = 4$. We can say that its radius is 2 units.
Then the area quarter circle is given by,
${A_1} = \dfrac{1}{4}\pi {r^2}$
On substituting value of r,
$\Rightarrow {A_1} = \dfrac{1}{4}\pi {\left( 2 \right)^2}$
On simplification we get,
$\Rightarrow {A_1} = \pi$
The area of the triangle is given by,
${A_2} = \dfrac{1}{2} \times b \times h$
As the h is 2 units and b is also 2 units, so we have,
$\Rightarrow {A_2} = \dfrac{1}{2} \times 2 \times 2$
On simplification we get,
$\Rightarrow {A_2} = 2$
Then the required area is given by,
$A = {A_1} - {A_2}$
$\Rightarrow A = \pi - 2$
Therefore, the required area is $\pi - 2$ square units.
As it is given to find the area by integration, we can use this method for verification of our answers.