Question

Using the method of integration find the area of the region bounded by the lines :
$2x+y=4$, $3x-2y=6$ and $x-3y+5=0$

Answer 1

Hint: First try to make a rough sketch of all the three lines and find their intersection points, two lines at a time. This would give us a triangle and its vertices. Now, break the entire area into two parts, according to the points of intersection and the valid lines that exist in that particular interval of $x$. Thus, break the integral up into two smaller intervals by looking at the diagram and proceed.

Complete Step-by-Step Solution:
Now, first let’s remember the formula that helped us find the area enclosed between two curves in a given interval.
If, $f(x)$ is the curve lying above $g(x)$ on the graph, then the formula of the area enclosed between the two of them in the interval $(a,b)$= $|\int\limits_{a}^{b}{(f(x)-g(x))dx}|$…(*)
We have to apply the same concept here. However, for this question, we first need to find the interval of integration. The first step to doing this would be finding the three points where the lines intersect each other, as only then we’ll have a triangle and be able to integrate.
Let’s call $2x+y=4$ equation (1), $3x-2y=6$ as equation (2), and $x-3y+5=0$ as equation (3).
To find the intersection point of (1) and (2), let’s multiply (1) by 2, and add it to (2). Doing so, we get :
$\begin{aligned} & (4x+2y)+(3x-2y)=8+6 \\\ & \Rightarrow 7x=14 \\\ & \Rightarrow x=2 \\\ \end{aligned}$
Now, for finding the corresponding value of $y$, let’s substitute this value of $x$ in (1). Doing so, we get :
$\begin{aligned} & 2x+y=4 \\\ & \Rightarrow 4+y=4 \\\ & \Rightarrow y=0 \\\ \end{aligned}$
Therefore, lines (1) and (2) intersect at (2,0).
Now, to find the intersection point of lines (2) and (3), let’s multiply (3) by 3 and subtract it from (2). Doing so, we get :
$\begin{aligned} & (3x-2y)-(3x-9y)=6+15 \\\ & \Rightarrow 7y=21 \\\ & \Rightarrow y=3 \\\ \end{aligned}$
Now, to find the corresponding value of $x$, let’s substitute this value of $y$ in (3). Doing so, we get :
$\begin{aligned} & x-3y+5=0 \\\ & \Rightarrow x-9+5=0 \\\ & \Rightarrow x=4 \\\ \end{aligned}$
Therefore, lines (2) and (3) intersect at (4,3).
Now, let’s find the intersection point of (1) and (3). Let’s multiply (1) by 3 and add it to (3). Doing so, we get :
$\begin{aligned} & (6x+3y)+(x-3y)=12-5 \\\ & \Rightarrow 7x=7 \\\ & \Rightarrow x=1 \\\ \end{aligned}$
Now, to find the corresponding value of $y$, let’s substitute this value of $x$ in (1). Doing so, we get :
$\begin{aligned} & 2x+y=4 \\\ & \Rightarrow 2+y=4 \\\ & \Rightarrow y=2 \\\ \end{aligned}$
Therefore, line (1) and line (3) intersect at (1,2).
Thus, we have the three intersection points for these three lines, forming a triangle. The points are point A (1,2), point B (2,0) and point C (4,3).
Now, let’s try to imagine what the figure looks like. Point A has the lowest $x$ coordinate, and is formed by the intersection of (1) and (3), point B is formed by the intersection of (1) and (2), and point C is formed by the intersection of (2) and (3). Let’s sketch the diagram now.

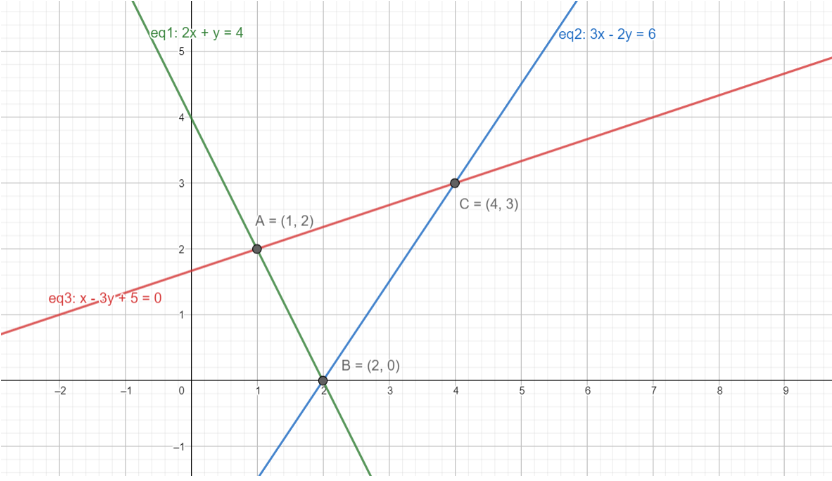
Here, we have all the three lines and the points signified clearly. Now, to find the area enclosed by the figure, we can easily integrate in the interval $x\in (1,4)$, since in this interval, the position of the curves relative to each other and the $x$ axis remains same, i.e. (3) stays above both, (1) and (2) in the interval $x\in (1,4)$. Before$x=1$, (1) is above (3), and after$x=4$, (2) becomes above (3), so we’ll need to change the expression under the integral unnecessarily because of the relative positioning of the lines. That’s why, it’s enough if we integrate from $x=1$ to $x=4$.
Now, to shorten our calculations, we can break the integral at the point $x=2$. Since from here, the relative positioning of (1) and (2) changes. (2) comes above (1), and so, it’ll be enough if we subtract the area covered by (2) from that covered by (3).
Therefore, we’ll use the formula $\int\limits_{a}^{c}{f(x)dx=\int\limits_{a}^{b}{f(x)dx+\int\limits_{b}^{c}{f(x)dx}}}$ provided $b$ lies between $a$ and $c$.
Here, $a=1,b=2,c=4$ .
Now, for the interval $x=1$ to $x=2$, going back to (), we’ll have the upper curve $\begin{aligned} & f(x)=line(3)=x-3y+5=0 \\\ & \Rightarrow f(x)=\dfrac{x+5}{3} \\\ \end{aligned}$ and the lower curve $\begin{aligned} & g(x)=line(1)=2x+y=4 \\\ & \Rightarrow g(x)=4-2x \\\ \end{aligned}$
Applying (), we get : Area1 = $\begin{aligned} & |\int\limits_{1}^{2}{(\dfrac{x+5}{3}-(4-2x))}dx|=|\int\limits_{1}^{2}{(\dfrac{x+5}{3}-4+2x)dx|} \\\ & =|\int\limits_{1}^{2}{\dfrac{x+5-12+6x}{3}}dx|=\dfrac{1}{3}|\int\limits_{1}^{2}{(7x-7)dx|} \\\ & =\dfrac{7}{3}|\int\limits_{1}^{2}{(x-1)dx}|=|\dfrac{7}{3}[\dfrac{{{x}^{2}}}{2}-x]_{1}^{2}| \\\ & =\dfrac{7}{3}|(\dfrac{4}{2}-2)-(\dfrac{1}{2}-1)|=\dfrac{7}{3}\times \dfrac{1}{2}=\dfrac{7}{6} \\\ \end{aligned}$
Now, for evaluating Area2, or the area enclosed between line (3) and line (2) in the interval $x=2$ to $x=4$.
Before applying (), let’s know the upper curve and the lower curve. Seeing the figure, we can clearly determine that the upper curve $\begin{aligned} & f(x)=line(3)=x-3y+5=0 \\\ & \Rightarrow f(x)=\dfrac{x+5}{3} \\\ \end{aligned}$ and the lower curve $\begin{aligned} & g(x)=line(2)=3x-2y=6 \\\ & \Rightarrow g(x)=\dfrac{3x-6}{2} \\\ \end{aligned}$.
Now, we can apply () here. Doing so, we’ll have Area2=$\begin{aligned} & |\int\limits_{2}^{4}{(f(x)-g(x))}dx|=|\int\limits_{2}^{4}{(\dfrac{x+5}{3}-\dfrac{3x-6}{2})}dx| \\\ & =|\int\limits_{2}^{4}{\dfrac{2x+10-(9x-18)}{6}dx}|=\dfrac{1}{6}|\int\limits_{2}^{4}{(28-7x)dx|} \\\ & =\dfrac{7}{6}|\int\limits_{2}^{4}{(4-x)dx|=\dfrac{7}{6}|[4x-\dfrac{{{x}^{2}}}{2}]_{2}^{4}|} \\\ & =\dfrac{7}{6}|(16-\dfrac{16}{2})-(8-\dfrac{4}{2})| \\\ & =\dfrac{7}{6}|8-6|=\dfrac{7}{6}\times 2=\dfrac{7}{3} \\\ \end{aligned}$
The last step is to find the final area, by adding Area1 and Area2, and find the total area enclosed in the interval $x=1$ to $x=4$, by the three lines.
Therefore, total Area = Area1+Area2 $=\dfrac{7}{6}+\dfrac{7}{3}=\dfrac{7}{3}(\dfrac{1}{2}+1)=\dfrac{7}{3}\times \dfrac{3}{2}=\dfrac{7}{2}$
Hence, our required area = $\dfrac{7}{2}$.