Question

Using the method of integration, find the area of the region bounded by the following lines:
$3x-y-3=0,2x+y-12=0,x-2y-1=0$.

Answer 1

First of all plot these straight lines on the graph paper and see the point of intersections of these lines and the area these lines are making. Then find the point of intersections of the three lines. We know that the area of a curve or a line in two dimensions is represented by $\int{ydx}$ within certain limits so the region which is bounded by these lines are the point of intersections of three lines so using this integration and applying certain limits we can find the area of the bounded region.

Complete step by step answer:
We have given three straight lines which we have shown below:
$\begin{aligned} & 3x-y-3=0.......Eq.(1) \\\ & 2x+y-12=0.........Eq.(2) \\\ & x-2y-1=0...........Eq.(3) \\\ \end{aligned}$
We have to find the area of the region bounded by these three lines using a method of integration.
First of all we have plotted these three straight lines on the graph we get,

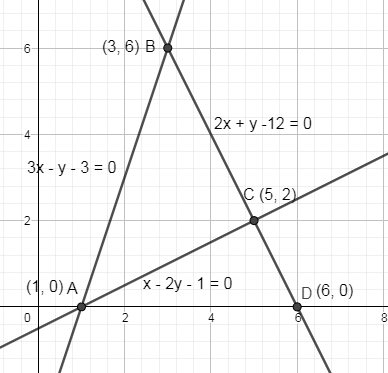
From the above figure, you can see that the area bounded by the three straight lines is a triangle ABC so we have to find this area of triangle ABC using the method of integration.
Now, we are going to find the point of intersections of these three lines as follows: Finding the intersection of eq. (1) and eq. (2) we get,
$\begin{aligned} & 3x-y-3=0 \\\ & 2x+y-12=0 \\\ \end{aligned}$
Adding above two equations we get,
$\begin{aligned} & 5x-15=0 \\\ & \Rightarrow 5x=15 \\\ \end{aligned}$
Dividing 5 on both the sides we get,
$\begin{aligned} & \dfrac{5x}{5}=\dfrac{15}{5} \\\ & \Rightarrow x=3 \\\ \end{aligned}$
Substituting the above value of x in eq. (1) we get,
$\begin{aligned} & 3\left( 3 \right)-y-3=0 \\\ & \Rightarrow 9-y-3=0 \\\ & \Rightarrow 6-y=0 \\\ & \Rightarrow y=6 \\\ \end{aligned}$
Intersection of eq. (1) and eq. (2) is $\left( 3,6 \right)$. Now, from the above figure, the point of intersection of eq. (1 and 2) is point B. Hence, we got the coordinates of point B $\left( 3,6 \right)$.
Now, finding the intersection of eq. (2 and 3) we get,
$\begin{aligned} & 2x+y-12=0.........Eq.(2) \\\ & x-2y-1=0...........Eq.(3) \\\ \end{aligned}$
Multiplying eq. (2) by 2 and then add in eq. (3) we get,
$\begin{aligned} & \left( 2x+y-12=0 \right)\times 2.........Eq.(2) \\\ & x-2y-1=0...........Eq.(3) \\\ \end{aligned}$
$\begin{aligned} & 4x+2y-24=0 \\\ & x-2y-1=0 \\\ \end{aligned}$
Adding the above equations we get,
$\begin{aligned} & 5x-25=0 \\\ & \Rightarrow 5x=25 \\\ \end{aligned}$
Dividing 5 on both the sides we get,
$\begin{aligned} & \dfrac{5x}{5}=\dfrac{25}{5} \\\ & \Rightarrow x=5 \\\ \end{aligned}$
Substituting the above value of x in eq. (2) we get,
$\begin{aligned} & 2\left( 5 \right)+y-12=0 \\\ & \Rightarrow 10+y-12=0 \\\ & \Rightarrow y-2=0 \\\ & \Rightarrow y=2 \\\ \end{aligned}$
The intersection of eq. (2 and 3) is the point C so we have got the coordinates of point C as $\left( 5,2 \right)$.
Finding the intersection of eq. (3 and 1) we get,
$\begin{aligned} & 3x-y-3=0.......Eq.(1) \\\ & x-2y-1=0...........Eq.(3) \\\ \end{aligned}$
Multiplying eq. (3) by 3 and then subtracting eq. (3) from eq. (1) we get,
$\begin{aligned} & \left( x-2y-1=0 \right)\times 3 \\\ & 3x-6y-3=0 \\\ \end{aligned}$
Subtracting the above eq. from eq. (1) we get,
$\begin{aligned} & -y+6y-3+3=0 \\\ & \Rightarrow 5y+0=0 \\\ & \Rightarrow y=0 \\\ \end{aligned}$
Substituting the above value of y in eq. (1) we get,
$\begin{aligned} & 3x-0-3=0 \\\ & \Rightarrow 3x=3 \\\ & \Rightarrow x=1 \\\ \end{aligned}$
As the intersection of eq. (1) and eq. (3) is the point A so the coordinates of point A is $\left( 1,0 \right)$.
We have got the coordinates of points A, B and C as:
$A\left( 1,0 \right),B\left( 3,6 \right),C\left( 5,2 \right)$
In the below figure, we have shown the point of intersections A, B and C.

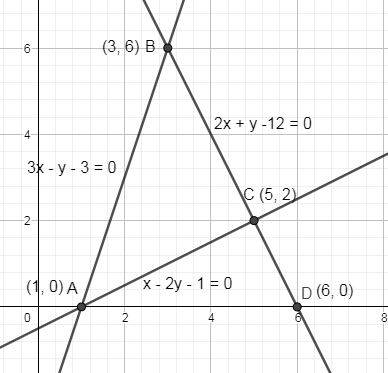
To find the area of the triangle ABC we have to find the area of the triangle ABD then subtract the area of the triangle ACD from it.
Now, we are going to find the area of the triangle ABD by a method of integration in which we add the area under the straight line of eq. (1) and the straight line of eq. (2).
Area under the straight line $3x-y-3=0$ between the values of x equal to 1 to 3 is as follows:
We know the area under the curve through integration is done as follows:
$\int{ydx}$
The above integration is in certain limits.
Now, finding y from $3x-y-3=0$ we get,
$\begin{aligned} & 3x-y-3=0 \\\ & \Rightarrow 3x-3=y \\\ \end{aligned}$
Substituting the above value of y in the above integration we get,
$\int{\left( 3x-3 \right)dx}$
Putting the lower limit of x as 1 and upper limit of x as 3 in the above integration we get,
$\begin{aligned} & \int\limits_{1}^{3}{\left( 3x-3 \right)dx} \\\ & =\int\limits_{1}^{3}{3xdx}-3\int\limits_{1}^{3}{dx} \\\ & =3\left| \dfrac{{{x}^{2}}}{2} \right|_{1}^{3}-3\left| x \right|_{1}^{3} \\\ \end{aligned}$
Applying the lower and upper limit we get,
$\begin{aligned} & \dfrac{3}{2}\left( {{\left( 3 \right)}^{2}}-1 \right)-3\left( 3-1 \right) \\\ & =\dfrac{3}{2}\left( 8 \right)-6 \\\ & =12-6 \\\ & =6 \\\ \end{aligned}$
Now, finding the area under the straight line $2x+y-12=0$ between the limits of x as 3 to 6 we get,
$\int{ydx}$
Finding y from 2x+y-12=0 we get,
$\begin{aligned} & 2x+y-12=0 \\\ & \Rightarrow 12-2x=y \\\ \end{aligned}$
Substituting the above value of y in the above integration we get,
$\int{\left( 12-2x \right)dx}$
Applying the limits of x as 3 to 6 we get,
$\begin{aligned} & \int\limits_{3}^{6}{\left( 12-2x \right)dx} \\\ & =\int\limits_{3}^{6}{12dx}-2\int\limits_{3}^{6}{xdx} \\\ & =12\int\limits_{3}^{6}{dx}-2\int\limits_{3}^{6}{xdx} \\\ & =12\left| x \right|_{3}^{6}-2\left| \dfrac{{{x}^{2}}}{2} \right|_{3}^{6} \\\ \end{aligned}$
Applying lower and upper limit in the above integration we get,
$\begin{aligned} & 12\left( 6-3 \right)-\dfrac{2}{2}\left( {{\left( 6 \right)}^{2}}-{{\left( 3 \right)}^{2}} \right) \\\ & =12\left( 3 \right)-\left( 36-9 \right) \\\ & =36-27 \\\ & =9 \\\ \end{aligned}$
Hence, the value of the area under the straight line $2x+y-12=0$ between the limits of x as 3 to 6 is equal to 9.
Area cannot be negative so we are taking the positive value of the above area which is +9.
Now, adding the areas that we have just calculated we get,
$\begin{aligned} & 9+6 \\\ & =15 \\\ \end{aligned}$
Hence, we have calculated the area of triangle ABD as $15\text{sq}\text{. units}$.
Now, finding the area of triangle ACD by adding the area under the straight line of eq. (3 and 2) in certain limits we get,
Finding the area under the straight line of $x-2y-1=0$ in the limits of x as 1 to 5 we get,
Writing y in terms of x we get,
$\begin{aligned} & x-2y-1=0 \\\ & \Rightarrow x-1=2y \\\ & \Rightarrow \dfrac{x-1}{2}=y \\\ \end{aligned}$
Now, finding the integration of above y between the limits of x as 1 to 5 we get,
$\begin{aligned} & \int\limits_{1}^{5}{\dfrac{x-1}{2}dx} \\\ & =\dfrac{1}{2}\int\limits_{1}^{5}{xdx}-\dfrac{1}{2}\int\limits_{1}^{5}{dx} \\\ & =\dfrac{1}{2}\left| \dfrac{{{x}^{2}}}{2} \right|_{1}^{5}-\dfrac{1}{2}\left| x \right|_{1}^{5} \\\ \end{aligned}$
Applying lower and upper limits we get,
$\begin{aligned} & \dfrac{1}{2}\left( \dfrac{1}{2} \right)\left( {{\left( 5 \right)}^{2}}-1 \right)-\dfrac{1}{2}\left( 5-1 \right) \\\ & =\dfrac{1}{4}\left( 24 \right)-\dfrac{1}{2}\left( 4 \right) \\\ & =6-2=4 \\\ \end{aligned}$
Hence, we got the area under the eq. (3) in the limits of x from 1 to 5 as 4 sq. units.
Finding the area under the straight line of eq. (2) in the limits of x from 5 to 6 we get,
Writing y in terms of x we get,
$\begin{aligned} & 2x+y-12=0 \\\ & \Rightarrow 12-2x=y \\\ \end{aligned}$
Now, finding the integration of above y between the limits of x as 1 to 5 we get,
$\begin{aligned} & \int\limits_{5}^{6}{\left( 12-2x \right)dx} \\\ & =12\int\limits_{5}^{6}{dx-}2\int\limits_{5}^{6}{xdx} \\\ & =12\left| x \right|_{5}^{6}-2\left| \dfrac{{{x}^{2}}}{2} \right|_{5}^{6} \\\ \end{aligned}$
Applying lower and upper limits we get,
$\begin{aligned} & 12\left( 6-5 \right)-\dfrac{2}{2}\left( {{\left( 6 \right)}^{2}}-{{\left( 5 \right)}^{2}} \right) \\\ & =12-\left( 36-25 \right) \\\ & =12-\left( 11 \right) \\\ & =1 \\\ \end{aligned}$
Adding the above two areas under the straight lines of eq. (3 and 2) we get,
$4+1=5$
Hence, we have got the area of triangle ACD as 5 sq. units.
Now, subtracting area of triangle ACD from triangle ABD we get,
$\begin{aligned} & 15-5 \\\ & =10 \\\ \end{aligned}$

Hence, we got the area bounded by the three straight lines as 40 sq. units.

Note: In this question, it is the requirement of the question to find the area of the bounded region using the method of integration. If it is not given then we can directly find the area of triangle ABD and ACD and then subtract the area of triangle ACD from triangle ABD.

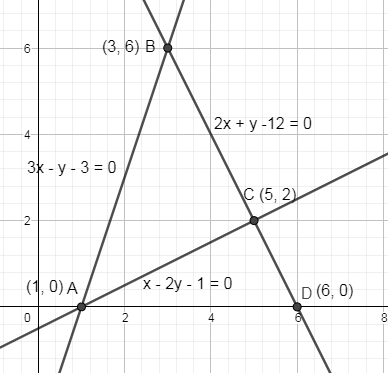
We know that area of a triangle is equal to:
$\dfrac{1}{2}\left( base \right)\left( height \right)$
In the area of triangle ABD, length of the base is 5 and length of the height is 6 which you can see from the figure so substituting these values in the above formula we get,
$\begin{aligned} & \dfrac{1}{2}\left( 5 \right)\left( 6 \right) \\\ & =5\left( 3 \right)=15 \\\ \end{aligned}$
Similarly, we can find the area of triangle ACD by using the formula for area of triangle as:
$\dfrac{1}{2}\left( base \right)\left( height \right)$
Substituting length of the base and height as 5 and 2 respectively we get,
$\begin{aligned} & \dfrac{1}{2}\left( 5 \right)\left( 2 \right) \\\ & =5 \\\ \end{aligned}$
Now, subtracting area of triangle ACD from triangle ABD we get,
$\begin{aligned} & 15-5 \\\ & =10 \\\ \end{aligned}$