Question
Question: Using the current division rule, find the current in each branch of the circuit shown in the figure....
Using the current division rule, find the current in each branch of the circuit shown in the figure.
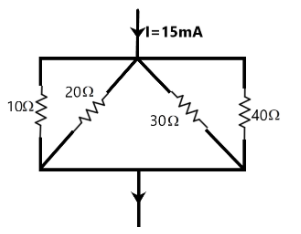
Solution
We need to understand the current divider rule used in the electric circuits in order to find the current through each of the given branches in the circuit. We need to know the method of application to solve this problem to get the value of current.
Complete Step-by-Step Solution: We are given a simple circuit in which an electric current of 15 mA flows into a junction which then gets split up into four different paths of different resistances. We know that the resistance of the path influences the current flowing through it. A larger resistance allows only a smaller current and vice versa. The current coming out at the end junction should be equal to the input current according to the Kirchhoff’s junction rule.
Now, the junction rule gives the current divider rule as –
Ix=IRxReq
From the above relation, we understand that we need to find the equivalent resistance of the given network in order to work on the current through each branch of the circuit as –
& \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+\dfrac{1}{{{R}_{4}}} \\\ & \Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{10}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{50} \\\ & \Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{30+15+10+6}{300} \\\ & \therefore {{R}_{eq}}=4.92\Omega \\\ \end{aligned}$$ Now, we can find the current through each of the branches using the current divider formula. Through the branch with resistance of $$10\Omega $$, we get – $$\begin{aligned} & {{I}_{1}}=I\dfrac{{{R}_{eq}}}{{{R}_{1}}} \\\ & \Rightarrow {{I}_{1}}=15mA\dfrac{4.92}{10} \\\ & \therefore {{I}_{1}}=7.38mA \\\ \end{aligned}$$ Through the branch with resistance of $$20\Omega $$, we get – $$\begin{aligned} & {{I}_{2}}=I\dfrac{{{R}_{eq}}}{{{R}_{2}}} \\\ & \Rightarrow {{I}_{2}}=15mA\dfrac{4.92}{20} \\\ & \therefore {{I}_{2}}=3.69mA \\\ \end{aligned}$$ Through the branch with resistance of $$30\Omega $$, we get – $$\begin{aligned} & {{I}_{3}}=I\dfrac{{{R}_{eq}}}{{{R}_{3}}} \\\ & \Rightarrow {{I}_{3}}=15mA\dfrac{4.92}{30} \\\ & \therefore {{I}_{3}}=2.46mA \\\ \end{aligned}$$ Through the branch with resistance of $$50\Omega $$, we get – $$\begin{aligned} & {{I}_{4}}=I\dfrac{{{R}_{eq}}}{{{R}_{4}}} \\\ & \Rightarrow {{I}_{4}}=15mA\dfrac{4.92}{50} \\\ & \therefore {{I}_{4}}=1.48mA \\\ \end{aligned}$$ So, we get the current through all the branches. This is the required solution. **Note:** We can see that the given circuit has all its resistances or the branches connected to two common nodes making the network a pure parallel combination of resistors which in turn results in the current division that is absent in a series combination.