Question

Using methods of coordinate geometry, Show that $\dfrac{{BP}}{{PC}} \times \dfrac{{CQ}}{{QA}} \times \dfrac{{AR}}{{RB}} = 1$ ,where $P$ , $Q$ , $R$ are the points of intersection of a line $l$ with the sides $BC$ , $CA$ , $AB$ of a triangle $ABC$ respectively.

Answer 1

Hint :To find the value of a given expression, we will use the concept of similar triangle property. To prove that two triangles are similar we will check for all the three corresponding angles of the triangle. We assume a certain constant for the different side such that the ratio of the corresponding side must be proportional.

Complete step-by-step answer :
The following is the schematic diagram of triangle ABC.

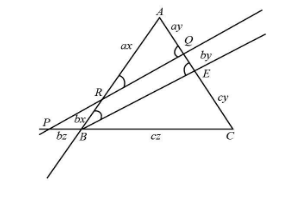
In order to draw a line $l$ which will intersect $BC$ , $CA$ , $AB$ we will have to extend the line segment $BC$ and $AB$ . Also, we will draw another line $BE$ parallel to line $RQ$ .
Now we will consider $\Delta ARQ$ and $\Delta ABE$ .
Since lines $RQ\parallel BE$ and $AB$ is the transversal, therefore corresponding angles will be equal.
Hence, $\angle ARQ = \angle ABE$
Since lines $RQ\parallel BE$ and $AE$ are the transversal, therefore corresponding angles will be equal.
Hence, $\angle AQR = \angle AEB$
Now $\angle A$ is the common angle in the triangles $\Delta ARQ$ and $\Delta ABE$ .
Hence, $\angle QAR = \angle EAB$
Therefore, $\Delta ARQ$ and $\Delta ABE$ are similar triangles through AAA congruency as all the angles are equal.
Hence, we can say that the sides of triangles $\Delta ARQ$ and $\Delta ABE$ will be in same proportion, that is,
$\dfrac{{AR}}{{AB}} = \dfrac{{AQ}}{{AE}}$
We can rearrange the above expression as,
$\dfrac{{AR}}{{AQ}} = \dfrac{{AB}}{{AE}}$
We can assume that this ratio is equal to $\dfrac{x}{y}$ ,such that,
$\dfrac{{AR}}{{AQ}} = \dfrac{{AB}}{{AE}} = \dfrac{x}{y}$
Now, we will assume a constant $a$ such that,
$\dfrac{{AR}}{{AQ}} = \dfrac{{ax}}{{ay}}$
We can consider $AR$ is $ax$ and $AQ$ is $ay$ .
Then we are assuming $bx$ for $BR$ then the value of $QE$ should be $by$ such that the ratio $\dfrac{{AB}}{{AE}}$ must be equals to $\dfrac{x}{y}$ as per our assumption. Since,
$\begin{array}{c} \dfrac{{AB}}{{AE}} = \dfrac{{AQ + QE}}{{AR + RB}}\\\ = \dfrac{{ax + bx}}{{ay + by}}\\\ = \dfrac{{x\left( {a + b} \right)}}{{y\left( {a + b} \right)}}\\\ = \dfrac{x}{y} \end{array}$
So according to our assumption we have $bx$ for $BR$ , $by$ for $QE$ , $ax$ for $AR$ and $ay$ for $AQ$ .
Similarly, we will consider triangles $\Delta CEB$ and $\Delta CQP$ .
Since lines $PQ\parallel BE$ and $CQ$ is the transversal, therefore corresponding angles will be equal.
Hence, $\angle CEB = \angle CQP$
Since lines $PQ\parallel BE$ and $CP$ is the transversal, therefore corresponding angles will be equal.
Hence, $\angle CBE = \angle CPQ$
Now $\angle C$ is the common angle in the triangles $\Delta CEB$ and $\Delta CQP$ .
Hence, $\angle QCP = \angle ECB$
Therefore, triangles $\Delta CEB$ and $\Delta CQP$ are similar triangles as all the angles are equal.
Hence, we can say that the sides of triangles $\Delta CEB$ and $\Delta CQP$ will be in same proportion.
$\dfrac{{CB}}{{CP}} = \dfrac{{CE}}{{CQ}}$
We can rearrange the above expression as.
$\dfrac{{CB}}{{CE}} = \dfrac{{CP}}{{CQ}}$
We can assume that this ratio is equal to $\dfrac{y}{z}$ .
$\dfrac{{CB}}{{CE}} = \dfrac{{CP}}{{CQ}} = \dfrac{z}{y}$
Now, we will assume a constant $c$ such that
$\dfrac{{CB}}{{CE}} = \dfrac{{cz}}{{cy}}$
We can consider $CB$ is $cz$ and $CE$ is $cy$ .
Then, $BP$ must be $bz$ such that the ratio $\dfrac{{CQ}}{{CP}}$ must be equals to $\dfrac{y}{z}$ as per our assumption.
Since,
$\begin{array}{c} \dfrac{{BP}}{{CQ}} = \dfrac{{CB + BP}}{{CE + QE}}\\\ = \dfrac{{cz + bz}}{{by + cy}}\\\ = \dfrac{{z\left( {c + b} \right)}}{{y\left( {c + b} \right)}}\\\ = \dfrac{z}{y} \end{array}$
So according to our assumption we have $bz$ for $BP$ , $cz$ for $CB$ and $cy$ for $CE$ .
Now we will substitute the values in the given expression,
$\begin{array}{l} \dfrac{{BP}}{{PC}} \times \dfrac{{CQ}}{{QA}} \times \dfrac{{AR}}{{RB}} = \dfrac{{bz}}{{\left( {b + c} \right)z}} \times \dfrac{{\left( {b + c} \right)y}}{{ay}} \times \dfrac{{ax}}{{bx}}\\\ \dfrac{{BP}}{{PC}} \times \dfrac{{CQ}}{{QA}} \times \dfrac{{AR}}{{RB}} = 1 \end{array}$
Hence, it is proved that $\dfrac{{BP}}{{PC}} \times \dfrac{{CQ}}{{QA}} \times \dfrac{{AR}}{{RB}} = 1$ .

Note : This question is based on the assumption and application of similar angled triangle concept. We will have to make correct assumptions such that the ratio of the sides remains proportional in the two similar triangles. Further we will put the assumed values in the given expression to prove the result.