Question

Using Kirchhoff’s rules determine the value of unknown resistance $R$ in the circuit so that no current flows through $4\Omega$ resistance. Also find the potential between A and D.

Answer 1

As a convention, for voltage sources, when moving from negative to positive add voltage when moving from positive to negative subtract voltage. For resistors, when moving in the same direction as conventional current, subtract voltage across the resistor but when moving in the opposite direction add voltage across the resistor.
Formula used: $\sum V = 0$ where $V$ is the voltage around a loop, $\sum {{I_{in}} = \sum {{I_{out}}} }$ where ${I_{in}}$ is the current flowing into a node and ${I_{out}}$ is the current flowing out of the node.

Complete step by step answer

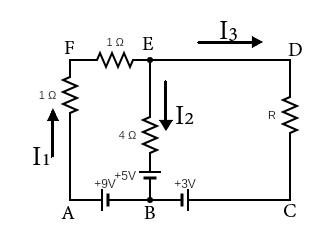
To solve, let us apply Kirchhoff’s voltage rule around the loop BAFEB, we have
$\Rightarrow 9 - {I_2}(1) - {I_1}(1) - {I_2} - 6 = 0$
$\Rightarrow 9 - 6 = 2{I_1} + {I_2} = 3$
Since ${I_2} = 0$, then
$\Rightarrow {I_1} = \dfrac{3}{2}$
$\Rightarrow 1.5A$
At node E,
$\Rightarrow {I_1} = {I_2} + {I_3}$
$\Rightarrow {I_1} = {I_3}$
Since ${I_2} = 0$, using the Kirchhoff’s voltage law on loop BAFDCB we get
$\Rightarrow 9 - {I_1} - {I_1} - {I_1}R - 3 = 0$
$\Rightarrow 6 - 2{I_1} = {I_1}R$
Making $R$ subject of the formula and inserting the values for ${I_1}$ we have
$\Rightarrow R = \dfrac{{6 - 2\left( {1.5} \right)}}{{1.5}}$
$\Rightarrow \dfrac{3}{{1.5}}$
$\Rightarrow 2\Omega$
The voltage between A and D is simply the voltage remained if we apply Kirchhoff’s law around a loop DCAFD but stop at point A. i.e.
$\Rightarrow {V_{DA}} = - {I_1}R - 3 + 9 = - {I_1}R + 6$
Inputting values of ${I_1}$ and $R$ again and solving, we get
$\Rightarrow {V_{DA}} = - 1.5\left( 2 \right) + 6$
$\Rightarrow - 3 + 6$
$\Rightarrow {V_{DA}} = 3V$
Hence, the required answer is 3V.

Additional Information
Kirchhoff’s rule is a physical principle which is more fundamental than Ohm’s law as it was derived from the principle of conservation of charge. In fact, it works with other elements besides resistors such as capacitors and inductors. It can also be used to analyze low frequency ac current.

Note
Alternatively, to find ${V_{DA}}$ we can take the path DFA instead of the path DCA as done above. Thus, we have,
$\Rightarrow {V_{DA}} = {I_1} + {I_1} = 2{I_1}$
The voltage difference across the $1\Omega$ resistors because we move in the direction opposite to the assumed conventional flow.
Substituting the value of ${I_1}$ in the above equation we get,
$\Rightarrow {V_{DA}} = 2\left( {1.5} \right) = 3V$
$\therefore {V_{DA}} = 3V$