Question

Using integration, prove that the curves ${y^2} = 4x$ and ${x^2} = 4y$ divide the area of the square bounded by $x = 0,x = 4,y = 0{\text{ and }}y = 4$ into 3 equal parts

Answer 1

Draw the ${y^2} = 4x$,${x^2} = 4x$ graph and the square bounded by the $4$ lines to get a visual image for reference. You will realise that the two curves divide the square into $3$ regions. You need to prove that each of these regions is$\dfrac{1}{3}{\text{rd}}$ of the area of the square. Integrate the area enclosed the${x^2} = 4y$curve against the $x$-axis and the area enclosed by the ${y^2} = 4x$curve against the $y$-axis separately. Also calculate the area of the square.
Given: We are given the curve ${y^2} = 4x$ and curve ${x^2} = 4y$
And the equations $x = 0$,$x = 4$,$y = 0$and $y = 4$that intersect to form a square.

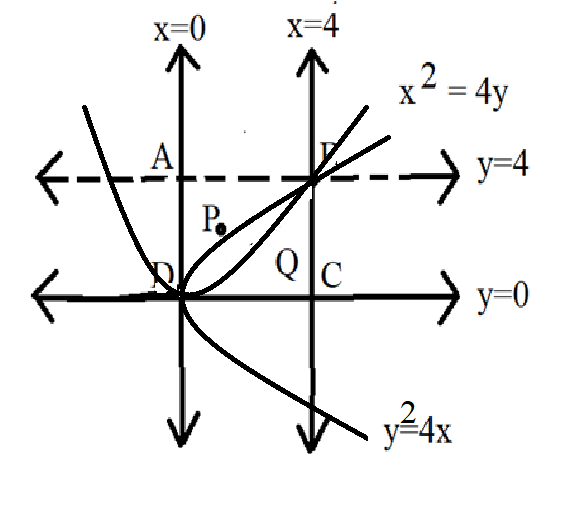
Complete step by step answer:
To prove that the area of the square is divided into $3$ parts by the curves.
That is, to prove that

$${\text{ar DABP = ar DPBQ = ar DQBC = }}\dfrac{1}{3}{\text{arABCD}} \\\ {\text{ar ABCD = 4}} \times 4 = 16 \\\$$

$\therefore \dfrac{1}{3}{\text{ar ABCD = }}\dfrac{{16}}{3} = 5.33\;\;\;\;\;\; \ldots \left( i \right)$
$ar{\text{ DABP}}$ is the area enclosed by the curve ${x^2} = 4y$ on the $x$-axis starting from $x = 0$to $x = 4$.
Similarly, $ar{\text{ DQBC}}$ is the area enclosed by the curve ${y^2} = 4x$ on the $y$-axis starting from $y = 0$ and $y = 4$.
To calculate ${\text{ar DQBC}}$,
${\text{ar DQBC = }}_0^4\smallint ydx$ [because area in on x-axis is]

$${x^2} = 4y \\\ \Rightarrow y = \dfrac{{{x^2}}}{4} \\\ \therefore {\text{ar DQBC = }}_0^4\smallint \dfrac{{{x^2}}}{4}dx \\\ = \dfrac{1}{4}\left[ {\dfrac{{{x^3}}}{3}} \right]_0^4 \\\$$

$= \dfrac{1}{{12}}\left( {{4^3}} \right) = \dfrac{{16}}{3}\;\;\;\;\;\;\; \ldots \left( {ii} \right)$
From $\left( i \right)$ and $\left( {ii} \right)$ we get
${\text{ar DQBC = }}\dfrac{1}{3}{\text{ar ABCD}}$
To calculate ${\text{ar DABP}}$,

$${\text{ar DABP = }}_0^4\smallint x{\text{dy}} \\\ {{\text{y}}^2} = 4x \\\ \Rightarrow x = \dfrac{{{y^2}}}{4} \\\ \therefore {\text{ar DABP = }}_0^4\smallint {\text{dy}} \\\ {\text{ = }}\dfrac{1}{4}\left[ {\dfrac{{{y^3}}}{3}} \right]_0^4 \\\$$

$= \dfrac{1}{{12}}\left( {{4^3}} \right) = \dfrac{{16}}{3}\;\;\;\;\;\; \ldots \left( {iii} \right)$
From $\left( i \right)$ and $\left( {iii} \right)$ we get,
${\text{ar DABP = }}\dfrac{1}{3}{\text{ar ABCD}}$
${\text{ar DQBC + ar DABP + ar DPBQ = ar ABCD}}$ [from $\left( i \right)$]
$\Rightarrow \dfrac{1}{3}{\text{ar ABCD + }}\dfrac{1}{3}{\text{ar ABCD + ar DPBQ = ar ABCD}}$
$\Rightarrow {\text{ar DPBQ = }}\dfrac{1}{3}{\text{ar ABCD}}\;\;\;\;\;\;\;\; \ldots \left( {iv} \right)$
From$\left( {ii} \right)$ , $\left( {iii} \right)$ and $\left( {iv} \right)$ we get
${\text{ar DABP = ar DPBQ = ar DQBC = }}\dfrac{1}{3}{\text{ABCD}}$.

Note:
You can calculate ${\text{ar DPBQ}}$by integrating the region ${\text{DPBC }}$and subtracting${\text{ar DQBC}}$ from it. However, it is evident from the diagram that the curves ${x^2} = 4y$ and ${y^2} = 4x$ divide the square into $3$ regions. So, it is sufficient to prove that ${\text{ar DABP = ar DQBC = }}\dfrac{1}{3}{\text{ABCD}}$ as it follows trivially that ${\text{ar DPBQ}}$must be ${\text{ar ABCD - ar DABP = ar DQBC = }}\dfrac{1}{3}{\text{ar ABCD}}$. The best way to solve coordinate geometry questions is to make a diagram and visualise areas from it.