Question

Using integration, find the area of the triangle whose vertices are A(2, 3), B(4, 7) and C(6, 2)

Answer 1

Hint: Geometrically, definite integration can be used to find the area under the given curve up to the x-axis. We will first find the equation of the sides of the triangle AB, BC and AC. An imaginary vertical line through B divides the figure in two parts. We will find the area under AB and BC. The extra area is removed by subtracting the area under AC, which will give us the final answer.The enclosing area is computed using the formula-

\mathop \smallint \nolimits_{{\text{x}} = {\text{a}}}^{{\text{x}} = {\text{b}}} {\text{f}}\left( {\text{x}} \right)d{\text{x}} = area

Complete step-by-step answer:

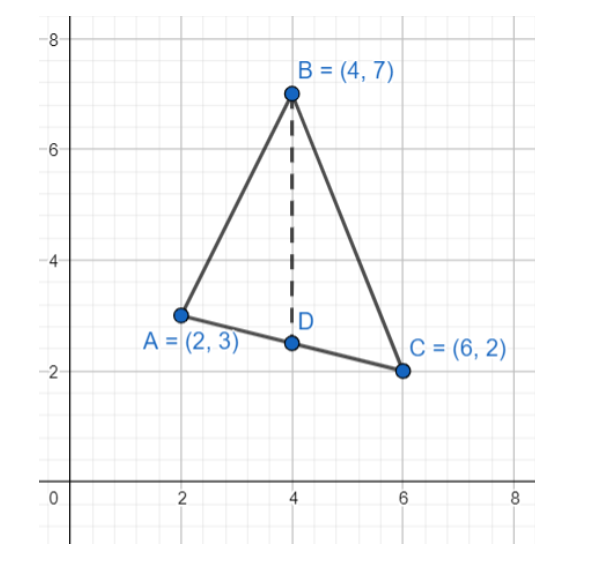
Using the two point form, the equation of the straight line is-
${\text{y}} - {{\text{y}}_1} = \dfrac{{{{\text{y}}_2} - {{\text{y}}_1}}}{{{{\text{x}}_2} - {{\text{x}}_1}}}\left( {{\text{x}} - {{\text{x}}_1}} \right)$
For line AB,
${\text{y}} - 3 = \dfrac{{7 - 3}}{{4 - 2}}\left( {{\text{x}} - 2} \right)$
${\text{y}} - 3 = 2{\text{x}} - 4$
${\text{y}} = 2{\text{x}} - 1...\left( 1 \right)$
For line BC,
${\text{y}} - 7 = \dfrac{{2 - 7}}{{6 - 4}}\left( {{\text{x}} - 4} \right)$
${\text{y}} - 7 = - \dfrac{5}{2}{\text{x}} + 10$
${\text{y}} = - \dfrac{5}{2}{\text{x}} + 17...\left( 2 \right)$
For line CA,
$y - 2 = \dfrac{{3 - 2}}{{2 - 6}}\left( {x - 6} \right)$
$y - 2 = - \dfrac{1}{4}x + \dfrac{3}{2}$
$y = - \dfrac{1}{4}x + \dfrac{7}{2}...\left( 3 \right)$
We will divide the triangle into two parts using the line x = 2, as shown in the figure. The first part has an area which is the difference of area under lines AB and AD. This is because the area under AB will give us the area down to the x-axis, but we don’t need that area. So we subtract the area under the line AD to get the area of the interior portion of the triangle. Similarly, the second part is an area with a difference of area under lines BC and DC.
So, for the first portion-
Area I = area under AB - area under AD
= \mathop \smallint \nolimits_2^4 \left( {2{\text{x}} - 1} \right)d{\text{x}} - \mathop \smallint \nolimits_2^4 \left( { - \dfrac{1}{4}{\text{x}} + \dfrac{7}{2}} \right)d{\text{x}}
$= \left( {{{\text{x}}^2} - {\text{x}}} \right)_2^4\; - \;\left( { - \dfrac{{{{\text{x}}^2}}}{8} + \dfrac{7}{2}{\text{x}}} \right)_2^4$
$= \left[ {16 - 4 - \left( {4 - 2} \right)} \right] - \left[ { - \dfrac{{16}}{8} + \dfrac{{28}}{2} - \left( { - \dfrac{4}{8} + \dfrac{{14}}{2}} \right)} \right]$
$= 10 - \left[ { - 2 + 14 + \dfrac{1}{2} - 7} \right]$
$= 10 - \dfrac{{11}}{2} = \dfrac{9}{2}$
For the second portion-
Area II = area under BC - area under DC
= \mathop \smallint \nolimits_4^6 \left( { - \dfrac{5}{2}{\text{x}} + 17} \right)d{\text{x}} - \mathop \smallint \nolimits_4^6 \left( { - \dfrac{1}{4}{\text{x}} + \dfrac{7}{2}} \right)d{\text{x}}
$= \left( { - \dfrac{5}{4}{{\text{x}}^2} + 17{\text{x}}} \right)_4^6 - \left( { - \dfrac{{{{\text{x}}^2}}}{8} + \dfrac{7}{2}{\text{x}}} \right)_4^6$
$= \left[ { - \dfrac{{180}}{4} + 102 - \left( { - \dfrac{{80}}{4} + 68} \right)} \right] - \left[ { - \dfrac{{36}}{8} + \dfrac{{42}}{2} - \left( { - \dfrac{{16}}{8} + \dfrac{{28}}{2}} \right)} \right]$
$= \left[ { - 45 + 102 - \left( { - 20 + 68} \right)} \right] - \left[ { - \dfrac{9}{2} + 21 - \left( { - 2 + 14} \right)} \right]$
$= 9 - \dfrac{9}{2} = \dfrac{9}{2}$
Area of the triangle is given by-
Area I + Area II = 9 sq units
This is the required answer.

Note: In such types of questions, we may need to divide the figure into two or more regions as shown in the figure. Also, a diagram is necessary to solve the problem correctly. Alternatively, we can use y-axis as the reference and then find the area of the triangle. The most common mistake is that the students forget to subtract areas under the line AC(AD + DC), which is wrong. If we just calculate the area under the line AB and BC, we are also including the area below the triangular region, till the x-axis, which is wrong.