Question

Using integration, find the area of the triangle$ABC$coordinates of whose vertices are $A\left( 4,1 \right),B\left( 6,6 \right)$ and $C\left( 8,4 \right)$.

Answer 1

First try to make a rough sketch. Now, break the entire area into two parts, according to the points of intersection. Thus, break the integral up into two smaller intervals by looking at the diagram and proceed.

Complete step-by-step answer:
First plot the points on a graph.

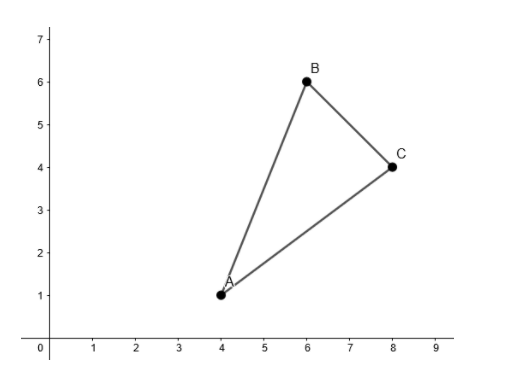
We know the equation of line between two points $({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})$ is given by the formula,
$y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x }_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right).........(i)$
Now using the above formula, equation of line $A\left( 4,1 \right),B\left( 6,6 \right)$ will be
$\Rightarrow y-1=\left( \dfrac{6-1}{6-4} \right)\left( x-4 \right)$
$\Rightarrow y-1=\left( \dfrac{5}{2} \right)\left( x-4 \right)$
On cross multiplication, we get

& \Rightarrow 2y-2=5x-20 \\\ & \Rightarrow 2y=5x-18 \\\ \end{aligned}$$ Dividing throughout by ‘2’, we get $$\Rightarrow y=\dfrac{5}{2}x-9........(ii)$$ Similarly, applying formula from equation (i), the equation of line $B(6,6),C(8,4)$ will be $$\begin{aligned} & y-6=\left( \dfrac{4-6}{8-6} \right)\left( x-6 \right) \\\ & \Rightarrow y-6=\dfrac{-2}{2}\left( x-6 \right) \\\ & \Rightarrow y-6=-1\left( x-6 \right) \\\ & \Rightarrow y-6=-x+6 \\\ \end{aligned}$$ $$y=-x+12........(iii)$$ Similarly, applying formula from equation (i), the equation of line $A(4,1),C(8,4)$ will be $$\begin{aligned} & y-1=\left( \dfrac{4-1}{8-4} \right)\left( x-4 \right) \\\ & \Rightarrow y-1=\dfrac{3}{4}\left( x-4 \right) \\\ \end{aligned}$$ On cross multiplication, we get $$\begin{aligned} & \Rightarrow 4y-4=3x-12 \\\ & \Rightarrow 4y=3x-12+4 \\\ \end{aligned}$$ Dividing throughout by ‘4’, we get $$y=\dfrac{3}{4}x-2.......(iv)$$ Now let’s remember the formula that helped us find the area enclosed between two curves in a given interval. If, $f(x)$ is the curve lying above $g(x)$ on the graph, then the formula of the area enclosed between the two of them in the interval $(a,b)=|\int\limits_{a}^{b}{(f(x)-g(x))dx}|$ Now, to find the area enclosed by the figure, we can easily integrate in the interval $x\in (4,8)$, since in this interval, the position of the curves relative to each other and the $x$ axis remains the same. Now, to shorten our calculations, we can break the integral at the point $x=6$. Since, from here the side of the triangle is changing. So area under side AB and BC, then we will subtract the area under the side AC. Therefore, we’ll use the formula $\int\limits_{a}^{c}{f(x)dx=\int\limits_{a}^{b}{f(x)dx+\int\limits_{b}^{c}{f(x)dx}}}$ provided $b$ lies between $a$ and $c$. Here, $a=4,b=6,c=8$ . So, area of triangle ABC is given by, $$=\int\limits_{4}^{6}{ydx+\int\limits_{6}^{8}{ydx-\int\limits_{4}^{8}{ydx}}}$$ Now substituting values from equation (ii), (iii) and (iv), we get $$\int\limits_{4}^{6}{\left( \dfrac{5}{2}x-9 \right)dx+\int\limits_{6}^{8}{\left( -x+12 \right)dx-\int\limits_{4}^{8}{\left( \dfrac{3}{4}x-2 \right)dx}}}$$ On integrating, we get $$\Rightarrow \left[ \dfrac{5{{x}^{2}}}{4}-9x \right]_{4}^{6}+\left[ \dfrac{-{{x}^{2}}}{2}+12x \right]_{6}^{8}-\left[ \dfrac{3{{x}^{2}}}{8}-2x \right]_{4}^{8}$$ Now applying the limit, we get $$\begin{aligned} & \Rightarrow \left[ \dfrac{5{{(6)}^{2}}}{4}-9(6) \right]-\left[ \dfrac{5{{(4)}^{2}}}{4}-9(4) \right]+\left[ \dfrac{-{{(8)}^{2}}}{2}+12(8) \right]-\left[ \dfrac{-{{(6)}^{2}}}{2}\\\\+12(6) \right]-\left[ \dfrac{3{{(8)}^{2}}}{8}-2(8) \right]+\left[ \dfrac{3{{(4)}^{2}}}{8}-2(4) \right] \\\ & \Rightarrow \left[ 45-54 \right]-\left[ 20-36 \right]+\left[ -32+96 \right]-\left[ -18+72 \right]-\left[ 24-16 \right]+\left[ 6-8 \right] \\\ & \Rightarrow -9+16+64-54-8-2 \\\ & \Rightarrow 7 \\\ \end{aligned}$$ Therefore the area of triangle ABC is 7 sq. units. **Note:** There are two alternate ways to do this sum. One is to apply heron’s formula and obtain the area of the triangle. But since it’s mentioned in the question that you have to use integration, you can’t use Heron’s formula here. Another alternate method is by integrating over the $y$ axis rather than the $x$ axis, i.e. finding out the area by integrating using $dy$ instead of $dx$. To do this however, you need to express each of the three lines as a function of $y$, rather than expressing them in terms of $x$, and you need to visualise which curve more to the right relative to the $y$ axis. The curve lying more to the right will be treated like the upper curve, and hence, we can find the area out in that way as well. But this will be complicated.