Question

Using integration, find the area of the region bounded by the parabola ${{\text{y}}^2} = 16{\text{x}}$ and the line x = 4.

Answer 1

Hint: Geometrically, definite integration can be used to find the area under the given curve up to the x-axis. We will first construct a figure of the parabola and the line, decide the limits of integration and then find the enclosing area using the formula-
\mathop \smallint \nolimits_{{\text{x}} = {\text{a}}}^{{\text{x}} = {\text{b}}} {\text{f}}\left( {\text{x}} \right)d{\text{x}} = area

Complete step-by-step answer:

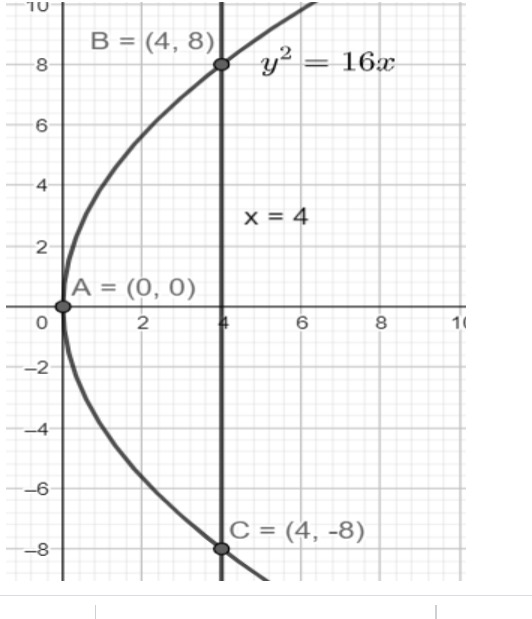
We can see that the enclosed region is divided into two equal parts by the x-axis. So, we will find the area of the upper region and then simply multiply it by two. First we will find the points of intersection of the line and the parabola, B and C.
${{\text{y}}^2} = 16{\text{x}}$
x = 4
Substituting the value of x-
${{\text{y}}^2} = 64$
${\text{y}} = \pm 8$
So the points are B(4, 8) and C(4, -8).
We know that-
${{\text{y}}^2} = 16{\text{x}}$
${\text{y}} = 4\sqrt {\text{x}}$
Now, the area of upper region will be given by-
Area = area under parabola under the limits x = 0 and x = 4.
= \mathop \smallint \nolimits_0^4 4\sqrt x dx\; = \;4\mathop \smallint \nolimits_0^4 \sqrt x dx
$= 4\left( {\dfrac{{2{x^{\dfrac{3}{2}}}}}{3}} \right)_0^4$
$= \dfrac{8}{3}\left( {{4^{\dfrac{3}{2}}} - 0} \right)$
$= \dfrac{8}{3} \times 8 = \dfrac{{64}}{3}$
This is the area of the upper region, the total area will be twice the area of the upper region. Hence the total area of the region bounded by the parabola and the line is-
$\dfrac{{64}}{3} \times 2 = \dfrac{{128}}{3}sq\;unit$

This is the required answer.

Note: In such types of questions, we may need to divide the figure into two or more regions as shown in the figure. Also, a diagram is necessary to solve the problem correctly. Alternatively, we can use y-axis as the reference and then find the area of the triangle.